Một sóng ngang hình sin truyền trên một sợi dây dài, biên độ dao động là 160 mm. Hình vẽ bên là hình dạng của một đoạn dây tại một thời điểm xác định. Trong quá trình lan truyền sóng, khoảng cách lớn nhất giữa hai phần tử M và N có giá trị gần nhất với giá trị nào sau đây?
.png)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiNếu không xét theo phương truyền sóng, hai điểm trên dây đang có sóng truyền qua có khoảng cách lớn nhất khi và chỉ khi hai điểm này tại cùng một thời điểm có li độ trái dấu nhưng cùng độ lớn (xM = –xN). Nghĩa là hai điểm này sẽ nằm đối xứng qua vị trí cân bằng.
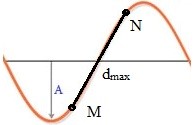
Dựa vào hình vẽ, ta có:
+ Độ dài của bước sóng: λ = 24 cm.
+ Khoảng cách giữa M và N: \(d=4.\frac{24}{12}=8\text{ cm}\text{.}\)
Khi hai điểm M và N đạt khoảng cách lớn nhất:
+ Khoảng cách của mỗi điểm so với vị trí cân bằng: \({{d}_{M}}={{d}_{N}}=\frac{8}{2}=4\text{ cm}\Rightarrow {{d}_{M}}={{d}_{N}}=\frac{\lambda }{6}.\)
+ Độ lớn li độ của điểm M và điểm N: \(\left| {{x}_{M}} \right|=\left| {{x}_{N}} \right|=\frac{A\sqrt{3}}{2}=\frac{1,6\sqrt{3}}{2}=\frac{4\sqrt{3}}{5}\text{ cm}\text{.}\)
Khoảng cách lớn nhất giữa M và N:
\({{d}_{\max }}=\sqrt{d_{M}^{2}+x_{M}^{2}}+\sqrt{d_{N}^{2}+x_{N}^{2}}=\sqrt{{{\left( \frac{4\sqrt{3}}{5} \right)}^{2}}+{{4}^{2}}}+\sqrt{{{\left( \frac{4\sqrt{3}}{5} \right)}^{2}}+{{4}^{2}}}\approx 8,5\text{ cm}\text{.}\)
.png)











