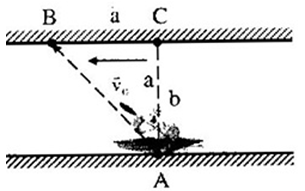
Ở một đoạn sông thẳng, dòng nước có vận tốc v0, một người từ vị trí A ở bờ sông này muốn chèo thuyền tới vị trí B ở bờ sông bên kia. Cho AC = 4,CB = 3. Độ lớn nhỏ nhất của vận tốc thuyền so với nước mà người này phải chèo đều để đến B là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:
+ Thuyền (1)
+ Dòng nước (2)
+ Bờ sông (3)
+ Vận tốc của thuyền (1) so với dòng nước (2): \( {v_{12}} = u\)
+ Vận tốc của dòng nước (2) so với bờ (3): \( {v_{23}} = v_0\)
+ Vận tốc của thuyền (1) so với bờ (2): \( {v_{13}} = v\)
- Vận dụng công thức cộng vận tốc, ta có:
\( \overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \leftrightarrow \vec v = \vec u + \overrightarrow {{v_0}} \)
Để thuyền đến được điểm B thì \( \vec v\) phải có hướng \( \overrightarrow {AB} \)
Từ hình ta thấy, \( {u_{\min }} \Leftrightarrow \vec u \bot \vec v\)
Ta suy ra:
\(\begin{array}{*{20}{l}} {{u_{\min }} = {v_0}\sin \alpha = {v_0}\frac{{AC}}{{AB}}}\\ { = {v_0}\frac{{AC}}{{\sqrt {A{C^2} + B{C^2}} }}}\\ { = {v_0}\frac{4}{{\sqrt {{4^2} + {3^2}} }} = 0,8{v_0}} \end{array}\)
Vậy để thuyền đến được điểm B thì vận tốc thuyền so với nước nhỏ nhất phải là \( {u_{\min }} = 0,8{v_0}\)
Đáp án cần chọn là: A