Trắc nghiệm Sự đồng biến, nghịch biến của hàm số Toán Lớp 12
-
Câu 1:
Cho hàm số y =f(x) có đồ thị của hàm số\(y=f^{\prime}(x) \) như hình vẽ bên. Hàm số \(y=f\left(3-x^{2}\right)\) đồng biến trên khoảng
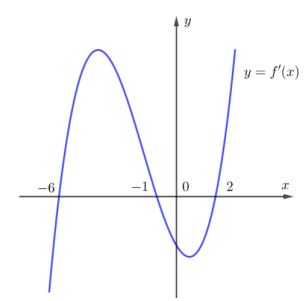
-
Câu 2:
Cho hàm số y=f(x) có đồ thị f '(x) như hình vẽ
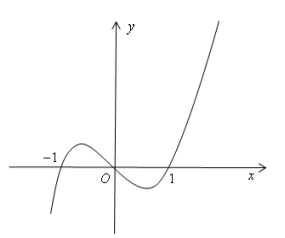
Hàm số \(f\left(x^{2}\right)\) đồng biến khoảng nào dưới đây?
-
Câu 3:
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x x^{2}(x-1)\left(x^{2}+m x+5\right)\). Có bao nhiêu số nguyên âm m để hàm số \(y=f\left(x^{2}\right)\)đồng biến trên khoảng \((1 ;+\infty)\)
-
Câu 4:
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x(x-1)^{2}\left(x^{2}+m x+9\right)\). Có bao nhiêu giá trị nguyên âm m để hàm số \(y=f(3-x)\) đồng biến trên khoảng \((0 ;+\infty)\).
-
Câu 5:
Cho hàm số y=f(x)có đạo hàm \(f^{\prime}(x)=x(x-1)^{2}\left(3 x^{4}+m x^{3}+1\right)\). Có bao nhiêu số nguyên âm m để hàm số \(y=f\left(x^{2}\right)\)đồng biến trên khoảng \((0 ;+\infty)\)
-
Câu 6:
Cho hàm số y=f(x) có đạo hàm\(f^{\prime}(x)=x\left(x^{2}-1\right)(x-4)\) . Hàm số y=f(3-x) đồng biến trên khoảng nào dưới đây?
-
Câu 7:
Cho hàm số y =f(x) có đồ thị f'(x) như hình vẽ bên
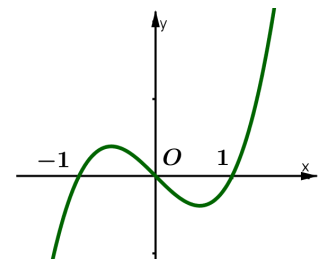
Hàm số \(y=f\left(x^{3}\right)\) đồng biến trên khoảng nào dưới đây? -
Câu 8:
Cho hàm số y =f(x) có đạo hàm \(f^{\prime}(x)=x^{2}(x-1)(x-4) g(x)\), trong đó \(g(x)>0, \forall x\) .Hàm số \(y=f\left(x^{2}\right)\) đồng biến trên khoảng nào dưới đây?
-
Câu 9:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây
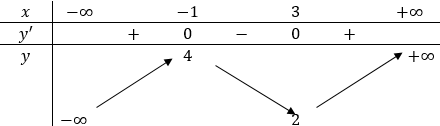
Hàm số y=f(3-x) đồng biến trên khoảng nào dưới đây?
-
Câu 10:
Cho hàm số y=f(x) có đạo hàm trên \(\mathbb{R}\) và có đồ thị hàm số y=f'(x) như hình vẽ.
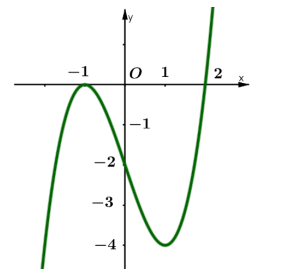
Đặt \(g(x)=f\left(x^{2}-2\right)\) Mệnh đề nào dưới đây sai?
-
Câu 11:
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x(x-1)^{2}(x-2)\). Hỏi hàm số \(y=f\left(\frac{5 x}{x^{2}+4}\right)\) đồng biến trên khoảng nào dưới đây?
-
Câu 12:
Cho hàm số y=f(x) có bảng biến thiên như sau
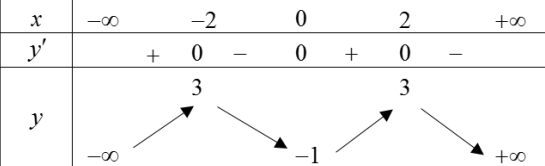
Hàm số \(y=f\left(x^{2}-2\right)\) nghịch biến trên khoảng nào dưới đây -
Câu 13:
Cho hàm số y=(x) có đạo hàm \(f'(x)=x^{2}(x-1)\left(x^{2}-4\right)\). Hàm số \(y=f(2-x)\) đồng biến trên khoảng
-
Câu 14:
Cho hàm số \(y=f(x)\). Hàm số\(y=f'(x)\) có đồ thị như hình vẽ bên. Hàm số \(y=f\left(x^{2}-2\right)\) đồng biến trên khoảng
.png)
-
Câu 15:
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình vẽ bên. Hàm số \(y=f(2-x)\) đồng biến trên khoảng
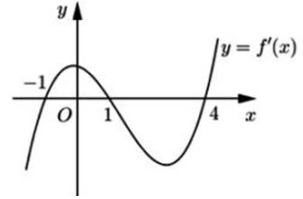
-
Câu 16:
Cho hàm số \(y=f(x)\). Đồ thị hàm số\(y=f^{\prime}(x)\) như hình vẽ bên. Hàm số \(g(x)=2 f(x)+(x+1)^{2}\) đồng biến trên khoảng nào?
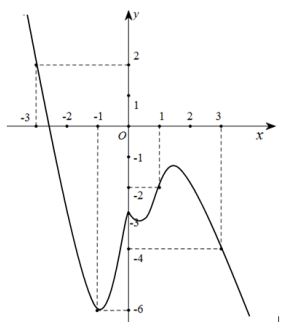
-
Câu 17:
Cho hàm số y =f(x) có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaceaa9qGaamiEaiabgkziUkabgUcaRiab % g6HiLcqabaGccaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaey % ypa0JaaGymaaaa!43B9! \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 1\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaceaa9qGaamiEaiabgkziUkabgkHiTiab % g6HiLcqabaGccaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaey % ypa0JaeyOeI0IaaGymaaaa!44B1! \mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 1\) . Khẳng định nào sau đây là đúng?
-
Câu 18:
Tìm tất cả giá trị thực của tham số m để hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqcLbAacaWG5b % Gaeyypa0JcdaWcaaqaaKqzGgGaaGymaaGcbaqcLbAacaaIZaaaaiaa % dIhakmaaCaaaleqabaGaaG4maaaajugObiabgkHiTiaaikdacaWGTb % GaamiEaOWaaWbaaSqabeaacaaIYaaaaKqzGgGaey4kaSIaaiikaiaa % d2gacqGHRaWkcaaIZaGaaiykaiaadIhacqGHRaWkcaWGTbGaeyOeI0 % IaaGynaaaa!4EA4! y = \frac{1}{3}{x^3} - 2m{x^2} + (m + 3)x + m - 5\) đồng biến trên R
-
Câu 19:
Hàm số \(y=\frac{x^{3}}{3}-\frac{m x^{2}}{2}-2 x+1\) đồng biến trên tập xác định khi:
-
Câu 20:
Giá trị nhỏ nhất của m để hàm số \(y=\frac{1}{3} x^{3}+m x^{2}-m x-m\) đồng biến trên \(\mathbb{R}\) là?
-
Câu 21:
Với giá trị nào của m hàm số \(y=\frac{m x+4}{x+m}\) nghịch biến trên từng khoảng xác định của nó:
-
Câu 22:
Tìm m để hàm số y\(y=x^{3}-3 m^{2} x\) đồng biến trên các khoảng xác định của nó
-
Câu 23:
Tìm m để hàm số \(y=\frac{x-m}{x+1}\) đồng biến trên từng khoảng xác định của chúng.
-
Câu 24:
Tìm tham số m để hàm số \(y=\frac{1}{3}(m-1) x^{3}+m x^{2}+(3 m-2) x\) là hàm đồng biến trên tập xác định của nó?
-
Câu 25:
Với giá trị nào của tham số m thì hàm số nghịch \(y=\frac{m x+3}{3 x+m}\) biến trên từng khoảng xác định của nó?
-
Câu 26:
Hàm số \(y=\frac{1}{3} x^{3}+(m+1) x^{2}-(m+1) x+1\) đồng biến trên tập xác định của nó khi?
-
Câu 27:
Tìm tham số m thì hàm số \(y=\frac{1}{3} x^{3}-m x^{2}+(2 m-1) x-m+2\) đồng biến trên R?
-
Câu 28:
Tìm tham số m để hàm số \(f(x)=-\frac{x^{3}}{3}+(m-1) x^{2}+(m+3) x\) đồng biến trên khoảng (0;3)
-
Câu 29:
Hàm số \(y=x^{2}+2(m-2) x+1\) đồng biến trên khoảng \((1;+\infty)\) khi:
-
Câu 30:
Với giá trị nào của m thì hàm số \(y=x^{3}-6 x^{2}+m x+1\) đồng biến trên khoảng \((0;+\infty)\)
-
Câu 31:
Hàm số \(y=\frac{x+2}{x-m}\) đồng biến trên khoảng \((2;+\infty)\) khi
-
Câu 32:
Tìm m để hàm số:\(y=2 x^{3}-3(2 m+1) x^{2}+6 m (m+1 )x+1\) đồng biến trên khoảng \((2 ;+\infty)\)
-
Câu 33:
Tìm m để hàm số \(y=-x^{3}+3 x^{2}+3 m x-1\) nghịch biến trên \((0;+\infty)\)
-
Câu 34:
Cho hàm số \(y=x^{3}+3 x^{2}-m x-4\) . Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng \((-\infty ; 0)\)
-
Câu 35:
Cho hàm số \(y=\frac{mx+2m–3}{x–m}\) (m là tham số). Tìm tất cả các giá trị của m sao cho hàm số nghịch biến trên khoảng \((2;+\infty)\)
-
Câu 36:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{x+2–2m}{x+m}\) đồng biến trên (–1;2).
-
Câu 37:
Tìm m để hàm số \(y=\frac{(m+1) x-1}{2 m x+1}\) đồng biến trên khoảng (0;1).
-
Câu 38:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{x}{x-m}\) đồng biến trên khoảng \((1 ;+\infty)\)
-
Câu 39:
Cho hàm số \(y=x^3-(m+1)x^2-(m^2-2m)x+2020\). Tìm m để hàm số nghịch biến trên khoảng (0;1)
-
Câu 40:
Cho hàm số \(y=\frac{3 x-2}{m x+1}\). Tìm m để hàm số đã cho đồng biến trên từng khoảng xác định.
-
Câu 41:
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaaeaaaaaaaaa8 % qacaWG5bGaeyypa0JaeyOeI0IaamiEa8aadaahaaWcbeqaa8qacaaI % 0aaaaOGaey4kaSIaaGioaiaadIhapaWaaWbaaSqabeaapeGaaGOmaa % aakiabgUcaRiaaiAdaaaa!3FD9! y = - {x^4} + 8{x^2} + 6\) đồng biến trên khoảng nào dưới đây?
-
Câu 42:
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaWG4bWaaWba % aSqabeaacaaIYaaaaOGaeyOeI0IaamiEaiabgUcaRiaaiodaaaa!404F! y = {x^3} - {x^2} - x + 3\) nghịch biến trên khoảng
-
Câu 43:
Hàm số nào sau đây luôn nghịch biến trên R
-
Câu 44:
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpdaWc % aaqaaiabgkHiTiaaikdaaeaacqGHsislcaWG4bGaey4kaSIaaGymaa % aaaaa!41AF! y = f\left( x \right) = \frac{{ - 2}}{{ - x + 1}}\) có tính chất
-
Câu 45:
Cho hàm số \(y=x^{3}+2(m+1) x^{2}-3 m x+5-m\) với m là tham số. tìm diều kiện của m đẻ hàm số đồng biến trên tập xác định?
-
Câu 46:
Cho hàm số \(y=\frac{mx+2–2m}{x+m}\,\,\,\,\,(1)\) (m là tham số). Tìm m để hàm số (1) đồng biến trên từng khoảng xác định.
-
Câu 47:
Điều kiện cần và đủ để hàm số \(y=\frac{m x+5}{x+1}\) đồng biến trên từng khoảng xác định là?
-
Câu 48:
Trong tất cả các giá trị của tham số m để hàm số \(y=\frac{1}{3}x^3+mx^2–mx–m \) đồng biến trên R, giá trị nhỏ nhất của m là?
-
Câu 49:
Tìm tham số m để hàm số \(y=\frac{1}{3}x^3+(m+1)x^2–(m+1)x+1\) đồng biến trên tập xác định.
-
Câu 50:
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaisdaaaGccqGHsislcaaI0aGaamiE % amaaCaaaleqabaGaaG4maaaakiabgUcaRiaaiodaaaa!3F24! y = {x^4} - 4{x^3} + 3\) đồng biến trên những khoảng nảo sau đây?











