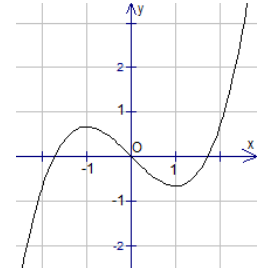
Cho hàm số y = f(x) có đạo hàm y = f'(x) liên tục trên \(\mathbb{R}\) và có đồ thị của hàm số y = f'(x) trên đoạn \(\left[ { – 2;6} \right]\) như hình vẽ bên.Cho hàm số y = f(x) có đạo hàm y = f'(x) liên tục trên \(\mathbb{R}\) và có đồ thị của hàm số y = f'(x) trên đoạn \(\left[ { – 2;6} \right]\) như hình vẽ bên.
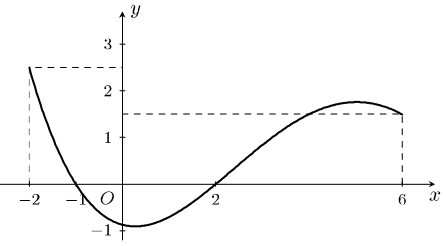
Tìm khẳng định đúng trong các khẳng định sau:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiLập bảng biến thiên của hàm số trên
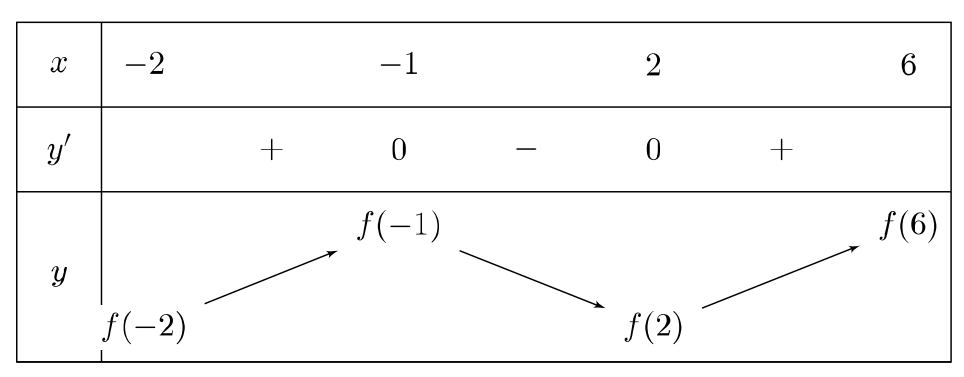
Dựa vào bảng biến thiên ta thấy:
Hàm số đồng biến trên \(\left( { – 2; – 1} \right)\) và \(\left( {2;6} \right)\).
Suy ra \(f\left( { – 1} \right) > f\left( { – 2} \right)\) và \(f\left( 6 \right) > f\left( 2 \right)\) (1)
Hàm số nghịch biến trên \(\left( { – 1;2} \right)\) suy ra \(f\left( { – 1} \right) > f\left( 2 \right)\).
Từ (1) và (2) suy ra :
\(\mathop {\max }\limits_{\left[ { – 2;6} \right]} f(x) = \max \left\{ {f( – 2);f( – 1);f(2);f(6)} \right\} = \max \left\{ {f( – 1);f(6)} \right\}\)
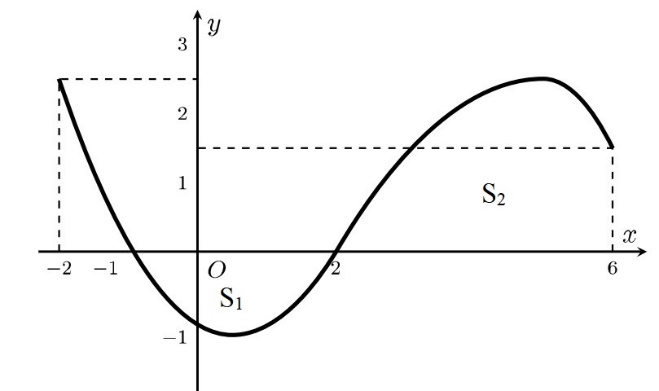
Ta có : \({S_1} = – \int\limits_{ – 1}^2 {f’\left( x \right)dx} = f\left( { – 1} \right) – f\left( 2 \right)\)
\({S_2} = \int\limits_2^6 {f’\left( x \right)dx = f\left( 6 \right) – f\left( 2 \right)} \)
Theo hình vẽ ta thấy \({S_1} < {S_2}\) nên \(f\left( { – 1} \right) – f\left( 2 \right) < f\left( 6 \right) – f\left( 2 \right) \Rightarrow f\left( { – 1} \right) < f\left( 6 \right)\).
Vậy \(\mathop {\max }\limits_{\left[ { – 2;6} \right]} f\left( x \right) = f\left( 6 \right)\).
Câu hỏi liên quan
-
Cho hàm số \(y = \left| {{x^4} - 4{x^3} + 4{x^2} + a} \right|\). Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M ≤ 2m?
-
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{5-4 x}\) trên đoạn [-1 ; 1] là:
-
Cho hàm số y=f(x) có đạo hàm và liên tục trên R. Biết đồ thị hàm số y=f′(x) như hình vẽ dưới. Xét hàm số \(g(x)=f^2(x)–3f(x)\). Biết\( f(2)=1, f(0)=–2, f(–1)=–3, f(3)=–1\), \(\mathop {\lim }\limits_{x \to \pm \infty } f(x) = - \infty \). Mệnh đề nào sau đây đúng?
-
Cho hàm số y=f(x) có đạo hàm cấp 2 trên , hàm số \(y=f^{\prime}(x)\) có đồ thị như hình vẽ bên
Giá trị lớn nhất của hàm số \(y=f\left(\frac{\sin x+\sqrt{3} \cos x}{2}\right) \text { trên đoạn }\left[-\frac{5 \pi}{6} ; \frac{\pi}{6}\right]\) bằng:
-
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên dưới. Biết rằng m là tham số thực, để giá trị nhỏ nhất của hàm số \(g\left( x \right) = f\left( {2x + 3} \right) + {x^2} – 4mx + 4{m^2} – 1\) bằng – 4 thì tham số m bằng
.jpg.png)
-
Giá trị lớn nhất của hàm số y=x3 −3x+5 trên đoạn \( \left[ {0;\frac{3}{2}} \right]\)
-
Tìm GTLN của hàm số \(y = x - \sqrt {{x^2} + 1} \) ?
-
Giá trị lớn nhất của hàm số \(y=\sqrt{-x^{2}+5 x}\) bằng
-
Hàm số \(y=\sin x+1\) đạt giá trị lớn nhất trên đoạn \(\left[-\frac{\pi}{2} ; \frac{\pi}{2}\right]\) bằng
-
Trên đoạn [-1;1], hàm số \(y = - \frac{4}{3} x³ - 2x² - x - 3\)
3 -
Giá trị nhỏ nhất của hàm số \(y=5 \sin x-\cos 2 x\) là:
-
Giá trị nhỏ nhất của hàm số \(y=x(x+2)(x+4)(x+6)+5\) trên nữa khoảng \([-4 ;+\infty)\)
-
Giá trị nhỏ nhất của hàm số \(f(x)=(x+1)(x+2)(x+3)(x+4)+2019\) là?
-
Giá trị nhỏ nhất của hàm số \(y = {x^3} + 3{x^2}\) trên đoạn \(\left[ { – 4; – 1} \right]\) bằng.
-
Hàm số \(y=\sin ^{2} x+2\) có giá trị nhỏ nhất, giá trị lớn nhất lần lượt bằng
-
Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số \(y = 2{x^3} + 3{x^2} – 12x + 1\) trên đoạn \(\left[ { – 1;3} \right].\) Khi đó tổng M + m có giá trị là một số thuộc khoảng nào dưới đây?
-
Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số\(g(x)=f\left(4 x-x^{2}\right)+\frac{1}{3} x^{3}-3 x^{2}+8 x+\frac{1}{3}\) trên đoạn [1;3]?
-
Hàm số \(y = 4\sqrt {{x^2} - 2x + 3} + 2x - {x^2}\) đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là
-
Cho hàm số \(y=\frac{x^{2}-3}{x-2}\). Khẳng định nào sau đây đúng về giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [3 ; 4]:
-
Giá trị nhỏ nhất của hàm số \(y=x+\frac{9}{x}\) trên đoạn [2;4] là:
