Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên \(S A=\frac{a \sqrt{2}}{2}\) tam giác SAC vuông tại S và nằm trong
mặt phẳng vuông góc với mặt đáy. Thể tích của khối chóp đã cho bằng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai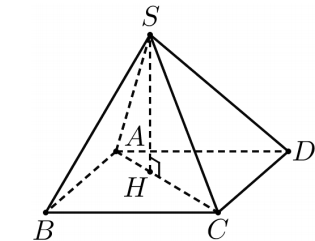
Kẻ \(S H \perp A C\).Từ giả thiết suy ra \(S H \perp(A B C D)\).
Trong tam giác vuông SAC, có \(A C=a \sqrt{2}\) và
\(\left\{\begin{array}{l} S A^{2}=A H \cdot A C \\ S H=\sqrt{S A^{2}-A H^{2}} \end{array} \Rightarrow\left\{\begin{array}{l} A H=\frac{a}{2 \sqrt{2}} \\ S H=\frac{a \sqrt{6}}{4} \end{array}\right.\right.\)
Vậy thể tích khối chóp: \(V_{S . A B C D}=\frac{1}{3} S_{A B C D} \cdot S H=\frac{a^{3} \sqrt{6}}{12}\)
ADMICRO
YOMEDIA
ZUNIA9