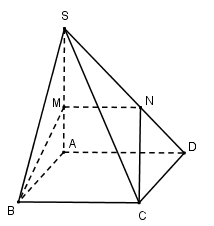
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và SA = a. Điểm M thuộc cạnh SA sao cho \( \frac{{SM}}{{SA}} = k\). Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Vì BC//AD nên mặt phẳng (BMC) cắt (SAD) theo đoạn thẳng MN//AD(N∈SD)
Vì
\(\begin{array}{l} MN//AD \Rightarrow \frac{{SM}}{{SA}} = \frac{{SN}}{{SD}} = k\\ \frac{{{V_{S.MBC}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}} = k \to {V_{S.MBC}} = k.{V_{S.ABC}} = \frac{k}{2}\\ \frac{{{V_{S.MNC}}}}{{{V_{S.ADC}}}} = \frac{{SM}}{{SA}}\frac{{SN}}{{SD}} = {k^2} \to {V_{S.MNC}} = {k^2}{V_{S.ADC}} = \frac{k}{2}{V_{S.ABCD}}\\ \to {V_{S.MBCN}} = {V_{S.MBC}} + {V_{S.MNC}} = \left( {\frac{k}{2} + \frac{{{k^2}}}{2}} \right){V_{S.ABCD}} \end{array}\)
Để mặt phẳng (BMNC) chia hình chóp thành 2 phần có thể tích bằng nhau thì
\( \frac{k}{2} + \frac{{{k^2}}}{2} = \frac{1}{2} \Leftrightarrow {k^2} + k - 1 = 0 \Leftrightarrow k = \frac{{ - 1 + \sqrt 5 }}{2}\) do k>0
Câu hỏi liên quan
-
Tìm số mặt phẳng đối xứng của khối bát diện đều.
-
Khối tứ diện đều là khối đa diện đều loại nào?
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt đáy nằm trong hình vuông ABCD. Biết rằng SA và SC tạo với đáy các góc bằng nhau, góc giữa SB và đáy bằng 450, góc giữa SD và đáy bằng \(\alpha\) với \( \tan \alpha = \frac{1}{3}\). Tính thể tích khối chóp đã cho
-
Hình đa diện nào sau đây không có mặt đối xứng?
-
Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
-
Tính diện tích toàn phần của hình lập phương có cạnh bằng 15 cm.
-
Cho phép vị tự tâm (O ) tỉ số (k < 0 ) lần lượt biến điểm (M,N ) thành (M',N' ), chọn mệnh đề sai:
-
Có bao nhiêu loại khối đa diện đều mà mỗi mặt của nó là một tam giác đều?
-
Khối đa diện đều loại (3;4) có tất cả bao nhiêu cạnh?
-
Số mặt phẳng đối xứng của tứ diện đều là
-
Hình lập phương có bao nhiêu mặt phẳng đối xứng?
-
Hình chóp tứ giác đều có mấy trục đối xứng?
-
Khối đa diện đều loại {3;5} là khối
-
Khối 12 mặt đều có bao nhiêu cạnh?
-
Trong các hình đa diện đều sau, hình nào có số đỉnh lớn hơn số mặt?
-
Cho hình chóp tứ giác đều S.ABCD. Nhận định nào sau đây không đúng :
-
Cho khối đa diện lồi có 8 mặt và 6 đỉnh. Số cạnh của nó là:
-
Hình lăng trụ tam giác đều có tất cả các cạnh bằng nhau có bao nhiêu mặt phẳng đối xứng?
-
Các mặt của khối 20 mặt đều là những đa giác nào?
-
Khối đa diện nào được cho dưới đây là khối đa diện đều?
