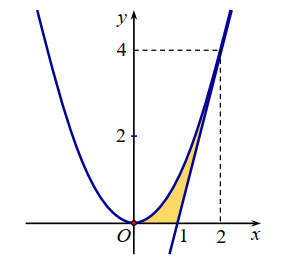
Cho hình (H ) giới hạn bởi trục hoành, đồ thị của một Parabol và một đường thẳng tiếp xúc với Parabol đó tại điểm A(2;4) , như hình vẽ bên. Thể tích vật thể tròn xoay tạo bởi khi hình (H ) quay quanh trục Ox bằng:

Câu hỏi liên quan

• Cho hàm số f (x) xác định trên \(\mathbb{R} \backslash\{-1 ; 1\}\) và thỏa mãn \(f^{\prime}(x)=\frac{1}{x^{2}-1} ; f(-3)+f(3)=0 \text { và } f\left(-\frac{1}{2}\right)+f\left(\frac{1}{2}\right)=2\). Tính giá trị biểu thức \(P=f(0)+f(4)\)?

• Tính tích phân \(I = \int\limits_0^1 {2{e^x}dx} \)

• Tính diện tích hình phẳng D giới hạn bởi các đường \(y = {\sin ^2}x\cos x,x = 0,x = \pi ,y = 0\)

ZUNIA12

• Cho \(I = \mathop \smallint \nolimits_1^{{e^{\frac{{\rm{\pi }}}{2}}}} \frac{{\cos \left( {\ln \;x} \right)}}{x}dx\), ta tính được:

• Thể tích khối tròn xoay khi quay quanh trục tung một hình phẳng giới hạn bởi hình tròn tâm I(2;0) bán kính R = 1 là:

• Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = √3 , biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục  tại điểm có hoành độ x (\(0 \le x \le \sqrt 3 \)) là một hình chữ nhật có độ dài hai cạnh là x và \(\sqrt {1 + {x^2}} \)

• Giả sử hàm số y =f(x)liên tục, nhận giá trị dương trên \((0 ;+\infty)\)và thỏa mãn \(f(x)=f^{\prime}(x) \sqrt{3 x+1}\) , với mọi x > 0 . Mệnh đề nào sau đây đúng? 

• Cho hàm số \(f(x) = \left\{ \begin{array}{l} 1 - {x^2}\,\,\,\,{\rm{khi}}\;x \le 3\\ 7 - 5x\,\,\,{\rm{khi}}\,\,x > 3 \end{array} \right.\). Tính tích phân \(\int\limits_{0}^{\ln 2}{f\left( 3{{e}^{x}}-1 \right)}{{\text{e}}^{x}}\text{d}x\).

• Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích của khối tròn xoay tạo thành được tính theo công thức nào?

  

• Cho \(\mathop \smallint \nolimits_0^3 f\left( x \right)dx = a,\;\mathop \smallint \nolimits_2^3 f\left( x \right)dx = b\). Khi đó \(\mathop \smallint \nolimits_0^2 f\left( x \right)dx\) bằng:

• Tính diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}, y=-\frac{1}{3} x+\frac{4}{3}\) và trục hoành.

• Trong các khẳng định sau, khẳng định nào sai?

• Tích phân \(I = \int\limits_0^1 {{{\rm{e}}^{2x}}{\rm{d}}x} \) bằng

• Cho hàm số y=f(x) và thỏa mãn \(f(x)-8 x^{3} f\left(x^{4}\right)+\frac{x^{3}}{\sqrt{x^{2}+1}}=0\). Tích phân \(I=\int_{0}^{1} f(x) d x=\frac{a-b \sqrt{2}}{c} \text { vói } a, b, c \in \mathbb{Z}\) và \(\frac{a}{c} ; \frac{b}{c}\)tối giản. Tính a+b+c

• Giá trị của tích phân \(I=\int\limits_{0}^{\frac{\pi}{2}}\left(\sin ^{4} x+\cos ^{4} x\right)\left(\sin ^{6} x+\cos ^{6} x\right) d x\) là

• Cho \(f\left( x \right), g\left( x \right)\) là hai hàm số liên tục trên đoạn \(\left[ { – 1;1} \right]\) và \(f\left( x \right)\) là hàm số chẵn, \(g\left( x \right)\) là hàm số lẻ. Biết \(\int\limits_0^1 {f\left( x \right){\rm{d}}x = 5} ;\int\limits_0^1 {g\left( x \right){\rm{d}}x = 7\,} \). Mệnh đề nào sau đây là sai?

• Tích phân \(I=\int_{0}^{1} \frac{a^{2} x^{3}+a x}{\sqrt{a x^{2}+1}} d x, \text { vói } a \geq 0\) có giá trị là:

• Diện tích hình phẳng giới hạn bởi đường cong \(y=x \ln x\), trục hoành và đường thẳng x=e là

• Gọi D là hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)=x^{2}-4 x+3\), trục hoành và hai đường thẳng \(x=1 ; x=3\). Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành bằng

• Nếu \(\int_0^2 {f\left( x \right){\rm{d}}x} = 2;\,\int_0^2 {g\left( x \right){\rm{d}}x} = 1\) thì \(\int_0^2 {\left[ {3f\left( x \right) – g\left( x \right)} \right]{\rm{d}}x} \) bằng