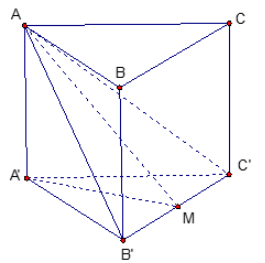
Cho lăng trụ đứng ABCA’B’C’ có đáy là tam giác đều cạnh a . Mặt phẳng (AB’C’) tạo với mặt đáy một góc 600. Thể tích khối lăng trụ ABCA’B’C’ theo a bằng:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi M là trung điểm của B’C’. Vì tam giác A’B’C’ đều ⇒A′M⊥B′C′(1)⇒A′M⊥B′C′(1)
AA′⊥(A′B′C′)⇒AA′⊥B′C′(2)AA′⊥(A′B′C′)⇒AA′⊥B′C′(2)
Từ (1) và (2) ⇒B′C′⊥(AA′M)⇒B′C′⊥AM
(AB′C′)∩(A′B′C′)=B′C′; (AB′C′)⊃AM⊥B′C′; (A′B′C′)⊃A′M′⊥B′C′
\( \Rightarrow \widehat {((AB\prime C\prime );(A\prime B\prime C\prime ))} = \widehat {(AM;A\prime M)} = \widehat {AMA\prime } = {60^0}\)
Tam giác A’MC’ vuông tại M \( \Rightarrow A'M = A'C'.\sin 60 = \frac{{a\sqrt 3 }}{2}\)
Tam giác AA’M vuông tại A
\(\begin{array}{l} \Rightarrow AA' = A'M.\tan 60 = \frac{{a\sqrt 3 }}{2}.\sqrt 3 = \frac{{3a}}{2}\\ \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = \frac{{3a}}{2}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{3{a^3}\sqrt 3 }}{8} \end{array}\)
Chọn đáp án A.