Đồ thị (C) của hàm số \(y=\frac{x+1}{x-2}\) có các đường tiệm cận là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTập xác định \(D=\mathbb{R} \backslash\{2\}\)
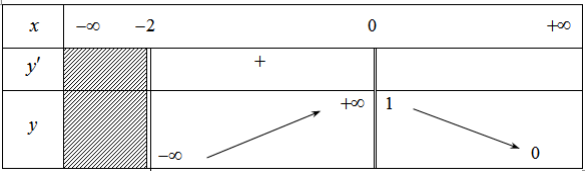
Ta có \(\lim\limits _{x \rightarrow 2^{+}} y=\lim\limits _{x \rightarrow 2^{+}} \frac{x+1}{x-2}=+\infty ; \lim\limits _{x \rightarrow 2^{-}} y=\lim \limits_{x \rightarrow 2^{-}} \frac{x+1}{x-2}=-\infty\) nên x = 2 là đường tiệm cận đứng của đồ thị hàm số.
Mặt khác \(\lim\limits _{x \rightarrow \pm \infty} y=\lim \limits_{x \rightarrow \pm \infty} \frac{x+1}{x-2}=1\) nên y =1 là đường tiệm cận ngang của đồ thị hàm số.
Câu hỏi liên quan
-
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHRaWkcaaIXaaabaGaamiEaiab % gkHiTiaaigdaaaaaaa!3E03! y = \frac{{2x + 1}}{{x - 1}}\). Đường tiệm cận đứng của đồ thị hàm số là:
-
Phương trình đường tiệm cận ngang của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaG4maiabgkHiTiaaisdacaWG4baabaGaeyOeI0Ia % aGOmaiaadIhacqGHRaWkcaaIXaaaaaaa!3FB0! y = \frac{{3 - 4x}}{{ - 2x + 1}}\) là:
-
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
-
Cho hàm số bậc ba \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9iaadggacaWG4bWaaWba % aSqabeaacaaIZaaaaOGaey4kaSIaamOyaiaadIhadaahaaWcbeqaai % aaikdaaaGccqGHRaWkcaWGJbGaamiEaiabgUcaRiaadsgaaaa!458D! f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4zamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaWaaeWaaeaa % caWG4bWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaG4maiaadIhacq % GHRaWkcaaIYaaacaGLOaGaayzkaaWaaOaaaeaacaaIYaGaamiEaiab % gUcaRiaaigdaaSqabaaakeaadaqadaqaaiaadIhadaahaaWcbeqaai % aaisdaaaGccqGHsislcaaI1aGaamiEamaaCaaaleqabaGaaGOmaaaa % kiabgUcaRiaaisdaaiaawIcacaGLPaaacaGGUaGaamOzamaabmaaba % GaamiEaaGaayjkaiaawMcaaaaaaaa!528F! g\left( x \right) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} - 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?
.png)
-
Với giá trị nào của m, đồ thị hàm số \(y = \frac{{x + 1 - \sqrt {{x^2} + 3x} }}{{{x^2} + \left( {m + 1} \right)x - m - 2}}\) có đúng hai đường tiệm cận?
-
Tìm tất cả các đường tiệm cận của đồ thị hàm số \(y=\frac{x+3}{\sqrt{x^{2}+1}}\)
-
Đồ thị hàm số nào sau đây không có tiệm cận ngang?
-
Tìm tiệm cận đứng của đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\)
-
Tìm số tiệm cận của đồ thị hàm số \(y=\frac{x^{2}-5 x+4}{x^{2}-1}\)
-
Tìm tất cả các tiệm cận đứng của đồ thị hàm số \(y=\frac{2 x-\sqrt{4 x^{2}-3 x+2}}{3 x^{2}-8 x+4}\)
-
Đồ thị hàm số \(y=\frac{\sqrt{x^{2}-4}}{x^{2}-5 x+6}\) có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
-
Tìm điểm M thuộc đồ thị hàm số \(y=\frac{2 x+1}{x-1}\) sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến trục hoành?
-
Số tiệm cận của đồ thị hàm số \(y=\left\{\begin{array}{l} \frac{\sqrt{x^{2}+1}}{x} \text { nếu } x \geq 1 \\ \frac{2 x}{x-1} \text { nếu } x<1 \end{array}\right.\) là
-
Cho hàm số y \(y=f(x) \text { có }\) có bảng biến thiên như hình vẽ dưới đây:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
-
Cho hàm số \(y=\frac{2 x-3}{x-2}(C)\). Gọi d là khoảng cách từ giao điểm của 2 tiệm cận của (C) đến một tiếp tuyến bất kỳ của đồ thị (C). Giá trị lớn nhất của d là
-
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên dưới:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y=\frac{1}{2 f(x)-1}\) là
-
Đồ thị hàm số \(y=x-\sqrt{x^{2}-4 x+3}\) có tiệm cận ngang là
-
Đồ thị hàm số \(y=x-\sqrt{x^{2}-4 x+2}\)có tiệm cận ngang là:
-
Đồ thị hàm số \(y=\frac{2 x-3}{x-1}\) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
-
Số đường tiệm cận của đồ thị hàm số \(y=\frac{\sqrt{x}}{x^{2}-1}\) là?
