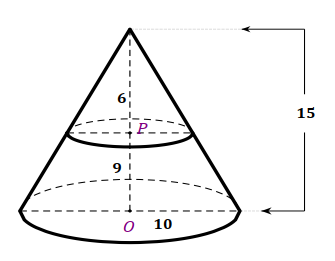
Hình nón có đường cao 20cm, bán kính đáy 25cm. Một mặt phẳng (P) qua đỉnh của hình nón và có khoảng cách đến tâm là 12cm. Diện tích thiết diện tạo bởi (P) và hình nón là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Theo đề bài ta có:
\(\begin{array}{l} \mathrm{h}=20, \mathrm{R}=25, \mathrm{OH}=12 \\ \mathrm{Ta} \mathrm{có}: \\ \frac{1}{\mathrm{OH}^{2}}=\frac{1}{\mathrm{SO}^{2}}+\frac{1}{\mathrm{OM}^{2}} \\ \Leftrightarrow \frac{1}{\mathrm{OM}^{2}}=\frac{1}{\mathrm{OH}^{2}}-\frac{1}{\mathrm{SO}^{2}} \Leftrightarrow \frac{1}{\mathrm{OM}^{2}}=\frac{1}{12^{2}}-\frac{1}{20^{2}}=\frac{1}{225} \\ \Rightarrow \mathrm{OM}=15 \end{array}\)
\(\begin{aligned} &\mathrm{SM}=\sqrt{\mathrm{SO}^{2}+\mathrm{OM}^{2}}=\sqrt{20^{2}+15^{2}}=25\\ &\mathrm{CD}=2 \mathrm{CM}=2 \sqrt{\mathrm{R}^{2}-\mathrm{OM}^{2}}=2 \sqrt{25^{2}-15^{2}}=40\\ &\text { Vậy } \mathrm{S}_{\Delta \mathrm{SCD}}=\frac{1}{2} \mathrm{SM} \cdot \mathrm{CD}=\frac{1}{2}. 40.25=500 . \text { Chọn dáp án B. } \end{aligned}\)
Câu hỏi liên quan
-
ho hình nón có đáy là đường tròn có đường kính 10. Mặt phẳng vuông góc với trục cắt hình nón theo giao tuyến là một đường tròn như hình vẽ. Thể tích của khối nón có chiều cao bằng 6 là?
-
Từ một tấm tôn hình chữ nhật kích thước 50cm x 240cm, 50cm x 240cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V1 là thể tích của thùng được theo cách 1 và V2 là tổng thể tích của hai thùng được theo cách 2. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)
-
Nếu cắt mặt trụ bởi mặt phẳng vuông góc với trục ta được là:
-
Một hình nón có đường kính của đường tròn đáy bằng 10 (cm) và chiều dài của đường sinh bằng 15 (cm). Thể tích của khối nón bằng.
-
Cho một khối trụ có bán kính đáy \(R=a\) và chiều cao \(h=2a\). Mặt phẳng \((P)\) song song với trục \(OO'\) của khối trụ chia khối trụ thành 2 phần, gọi \({{V}_{1}}\) là thể tích phần khối trụ chứa trục \(OO'\), \({{V}_{2}}\) là thể tích phần còn lại của khối trụ. Tính tỉ số \(\frac{{{V}_{1}}}{{{V}_{2}}}\), biết rằng \((P)\) cách \(OO'\) một khoảng bằng \(\frac{a\sqrt{2}}{2}\).
-
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng \(60^o\) . Thể tích khối nón nội tiếp trong hình chóp là:
-
Cho tam giác ABH vuông tại H , AH=3a , BH=2a. Quay tam giác ABH quanh trục AH ta được một khối nón có thể tích là:
-
Cho hình trụ có bán kính đáy bằng (a ) và chiều cao bằng (2a. ) Diện tích toàn phần của hình trụ bằng:
-
Cho hình trụ có bán kính đáy bằng (1 ) và chiều cao bằng (3 ). Thiết diện của hình trụ cắt bởi mặt phẳng qua trục của nó có diện tích bằng:3
-
Cho hình nón có đường sinh bằng \(\sqrt 3 a,\) chiều cao là a. Tính bán kính đáy của hình nón đó theo a.
-
Cho hình chóp S.ABC có SA = 8, SA vuông góc với đáy. Tam giác ABC vuông tại A, BC = 7. Tính bán kính của mặt cầu ngoại tiếp khối chóp.
-
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục (DF )
-
Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của khối trụ. Biết AD = 12 và góc ACD bằng \(60^0\). Thể tích của khối trụ là:
-
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S1 là diện tích 6 mặt của hình lập phương, S2 là diện tích xung quanh của hình trụ. Tỉ số \( \frac{{{S_2}}}{{{S_1}}}\) bằng:
-
Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của khối trụ. Biết AB = 4a, BC = 3a. Tính thể tích của khối trụ.
-
Cho \(AA'B'B\) là thiết diện song song với trục OO’ của hình trụ (A, B thuộc đường tròn tâm O). Cho biết \(AB=4,\text{AA }\!\!'\!\!\text{ =3}\) và thể tích của hình trụ bằng \(V=24\pi .\) Khoảng cách d từ O đến mặt phẳng \(\left( \text{AA}'B'B \right)\) là:
-
Cho tam giác ABC vuông tại B có \(AC = 2a,\,BC = a\), khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng:
-
Cho khối trụ \(\left( T \right)\) có bán kính đáy R = 1, thể tích \(V = 5\pi \). Tính diện tích toàn phần của hình trụ tương ứng
-
Diện tích xung quanh của mặt trụ có bán kính đáy R, chiều cao h là
-
Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R . Biết SO = h. Độ dài đường sinh của hình nón bằng
