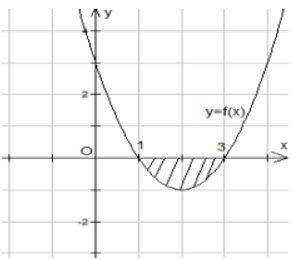
Hình phẳng giới hạn bởi đồ thị hàm số \(y=\frac{10}{3} x-x^{2} \text { và } y=\left\{\begin{array}{ll} -x & \text { khi } x \leq 1 \\ x-2 & \text { khi } x>1 \end{array}\right.\) có diện tích là:

Sân trường THPT Chuyên Hà Giang có một bồn hoa hình tròn có tâm O. Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này chia bồn hoa thành bốn phần, bởi hai đường Parabol có cùng đỉnh O và đối xứng nhau qua O. Hai đường Parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích (S₁,S₃ ) dùng để trồng hoa, phần diện tích  (S₂,S₄ ) dùng để trồng cỏ (Diện tích được làm tròn đến hàng phần trăm). Biết kinh phí trồng hoa là (150.000 ) đồng/ (m² ), kinh phí trồng cỏ là (100.000 ) đồng/ (m² ). Hỏi cả trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn).

Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) hàm số \(y = - {x^4} + 5{x^2} - 4\) với trục hoành.

Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn giới hạn bởi đường tròn \(x^2+y^2=16\) (nằm trong mặt phẳng Oxy), cắt vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện là hình vuông. Thể tích của vật thể là

Bạn Minh ngồi trên một máy bay đi du lịch thế giới với vận tốc chuyển động của máy bay là \(v(t)=3 t^{2}+5(m / s)\). Quãng đường máy bay đi được từ giây thứ thứ 5 đến giây thứ 10 là

Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi \(\displaystyle  {x^2} + {y^2} = 1\). Mỗi thiết diện vuông góc với trục \(\displaystyle  Ox\) là một hình vuông.

Một vật đang chuyển động đều với vận tốc \(v_{0}(m / s)\) thì bắt đầu tăng tốc với gia tốc \(a(t)=v_{0} t+t^{2}\left(m / s^{2}\right)\) trong đó t là khoảng thời gian được tính bằng giây kể từ thời điểm vật bắt đầu tăng tốc. Biết quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100m. Tính vận tốc ban đầu v₀ của vật.

Cho hàm số \(y=(x-2)^{2}\) có đồ thị (C) , khối tròn xoay tạo thành khi quay hình phẳng giới
hạn bởi (C) , trục Ox , trục Oy và đường thẳng x = 3 có thể tích là

Một ô tô đang chạy với vận tốc \(\displaystyle  10m/s\) thì người lái đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(\displaystyle  v\left( t \right) =  - 5t + 10\left( {m/s} \right)\), trong đó \(\displaystyle  t\) là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển bao nhiêu mét?

Cho hình phẳng giới hạn (H) như hình vẽ bên. Thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) quanh trục Oy là

Một vật chuyển động trong 3 giờ với vận tốc v(km/h)  phụ thuộc thời gian t (h) có đồ thị của vận tốc như hình vẽ bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I (2;9) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật di chuyển được trong 3 giờ đó (kết quả làm tròn hàng phần trăm):

Quay hình phẳng GG giới hạn bởi các đường y=x³,y=1,x=0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng

Cho hàm số y=f( x) liên tục và có đồ thị như hình bên. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục Ox. Quay hình phẳng D quanh trục Ox ta được khối tròn xoay có thể tích V được xác định theo công thức

Thể tích của khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường \(y=\sqrt{x}\) và y=x quanh trục Ox bằng

Quay hình phẳng G giới hạn bởi các đường y=x3,y=1,x=0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng:

Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục \(\displaystyle  Ox\) hình phẳng giới hạn bởi các đường \(\displaystyle  y = \frac{1}{x}\), \(\displaystyle  y = 0,x = 1\) và \(\displaystyle  x = a\left( {a > 1} \right)\). 

Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=\sqrt{x+1}\) và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ có đường kính lần lượt là 2dm và 4dm, khi đó thể tích của lọ là:

Một vật bắt đầu chuyển động với phương trình vận tốc là \(v(t)=\frac{2 t}{t^{2}+1}\) Hỏi từ lúc bắt đầu chuyển động đến khi vật có gia tốc nhỏ nhất đã đi được quãng đường dài bao nhiêu? 

Tính diện tích hình phẳng giới hạn bởi các đường sau: \(\displaystyle  y = x - 1 + \frac{{\ln x}}{x},y = x - 1\) và \(\displaystyle  x = e\)

Con cá bơi có phương trình quãng đường \(s(t)=-\frac{1}{10} t^{2}+4 t(\mathrm{~km})\), t tính bằng giờ. Biết con cá bơi xuôi dòng nước với tốc độ dòng chảy là 2 / km h . Tính khoảng cách xa nhất con cá bơi được? 

Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x = 0\) và \(x = \pi \), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\;(0 \le x \le \pi )\) là một tam giác đều cạnh  \(2\sqrt {{\mathop{\rm s}\nolimits} {\rm{inx}}} \).