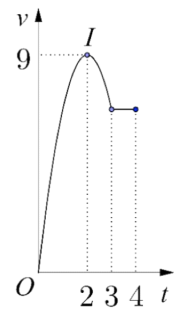
Một vật chuyển động trong 4 giờ với vận tốc v(km/h) phụ thuộc thời gian t(h ) có đồ thị của vận tốc như hình vẽ bên. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I ( 2;9) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật di chuyển được trong 4 giờ đó.

 

Một đám vi khuẩn tại ngày thứ x có số lượng là N(x). Biết rằng N'(x) = \(\frac{{2000}}{{1 + x}}\) và lúc đầu số lượng vi khuẩn là 5000 con. Vậy ngày thứ 12 số lượng vi khuẩn (sau khi làm tròn) là bao nhiêu con?

Quay hình phẳng Q giới hạn bởi các đường \( {y_2} = \frac{{2x}}{\pi };{y_1} = \sin x\) quanh trục Ox, ta được một khối tròn xoay. Khi đó thể tích của khối tròn xoay này bằng

Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người). Tìm khoảng thời gian T sao cho số lượng trẻ được sinh ra là 14 triệu kể từ khi kết thức chiến tranh.

Diện tích của hình phẳng giới hạn bởi các đường \(y = x^2+ 1 , y = 0, x = - 1, x = 2 \) bằng:

Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đường elip ( E) : \(x^{2}+9 y^{2}=9\) quay quanh Ox bằng

Cho hình (H) giới hạn bởi đồ thị hàm số y = x³, trục hoành và hai đường thẳng x = 0,x = 1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox được tính bởi:

Diện tích hình phẳng giới hạn bởi các đường \(y = x^2 - x , y = 2x - 2 , x = 0 , x = 3\) được tính bởi công thức:

Cho hình H giới hạn bởi đồ thị hàm số x = f(y) , trục tung và hai đường thẳng y = a,y = b. Thể tích khối tròn xoay tạo thành khi quay H  quanh trục Oy là:

Tính diện tích hình phẳng giới hạn bởi các đường sau:

\(\displaystyle  y = {x^3} - {x^2}\) và \(\displaystyle  y = \frac{1}{9}(x - 1)\)

Một xe lửa chuyển động chậm dần đều và dừng hẳn sau 20 giây kể từ khi bắt đầu hãm phanh. Trong thời gian đó xe chạy được 120m . Cho biết công thức vận tốc của chuyển động biến đổi đều là \(v(t)=v_{0}+a t(\mathrm{~m} / \mathrm{s})\) , trong đó \(a\left(\mathrm{~m} / \mathrm{s}^{2}\right)\) là gia tốc và v(m/s) là vận tốc tại thời điểm t(s ) . Hãy tính vận tốc v₀ lúc bắt đầu hãm phanh 

Cho hình phẳng giới hạn (H) như hình vẽ bên. Thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) quanh trục Oy là

Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f( x)\), đường thẳng (y = 0 ) và hai đường thẳng \(x = a,x = b(a < b)\) là:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3} - 4x\), trục hoành, đường thẳng x=-2 và đường thẳng x=4

Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x = -1\) và \(x = 1\), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x( - 1 \le x \le 1)\) là một hình vuông cạnh là \(2\sqrt {1 - {x^2}} \).

Cho hai hàm số f( x ) =  - x  và g( x ) = e^x. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y = f( x ),y = g( x ) và hai đường thẳng x = 0,x = e là:

Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(x=g(y)\), trục tung và hai đường thẳng \(y=a, y=b\) , như hình vẽ bên. Khẳng định nào sau đây đúng?

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3} - 3{x^2} + 2x\), trục hoành, trục tung và đường thẳng x = 3.

Một tập đoàn định đầu tư vào hai dự án. Giả sử, dự án đầu tư đầu có tốc độ sinh lợi nhuận là \(P_{1}(t)=50+t^{2}(\text { đồng/năm) }\), dự án thứ hai có tốc độ sinh lợi nhuận là \(P_{2}(t)=200+5 t(\text { đồng/năm) }\). Sau t năm thì tốc độ sinh lợi của dự án hai bằng một nửa dự án một. Tính lợi nhuận thực tế trong khoảng thời gian trên. 

Một vật đang chuyển động đều với vận tốc \(v_{0}(m / s)\) thì bắt đầu tăng tốc với gia tốc \(a(t)=v_{0} t+t^{2}\left(m / s^{2}\right)\) trong đó t là khoảng thời gian được tính bằng giây kể từ thời điểm vật bắt đầu tăng tốc. Biết quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100m. Tính vận tốc ban đầu v₀ của vật.

Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng xác định bởi \(\displaystyle  y = {x^{\frac{2}{3}}},x = 0\) và tiếp tuyến với đường \(\displaystyle  y = {x^{\frac{2}{3}}}\) tại điểm có hoành độ \(\displaystyle  x = 1\), quanh trục \(\displaystyle  Oy\)