Muốn làm một bồn chứa 1000 lít hình trụ có nắp đậy. Hỏi chiều cao h (dm) của bồn là để ít tốn vật liệu nhất. Gần với giá trị nào nhất
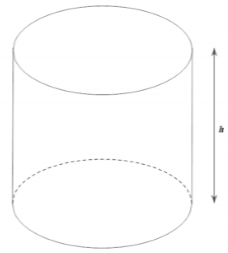
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐể ít tốn vật liệu nhất thì diện tích toàn phần bồn nước phải nhỏ nhất.
Tức là Stp = 2πR2+ 2πRh nhỏ nhất ( với R là bán kính đường tròn đáy)
Thể tích bồn nước: \(V = \;\pi {R^2}h\; = \;1000\; \Rightarrow \;R\; = \;\sqrt {\frac{{1000}}{{\pi h}}} \)
Khi đó :
\(\begin{array}{l}
{S_{tp}} = 2\pi .\frac{{1000}}{{\pi h}} + 2\pi \sqrt {\frac{{1000}}{{\pi h}}.h} = \frac{{2000}}{h} + \sqrt {4000\pi h} \\
S{'_{tp}} = - \frac{{2000}}{{{h^2}}} + \frac{{2000\pi }}{{\sqrt {4000\pi h} }}\\
S{'_{tp}} = 0 \Leftrightarrow \sqrt {4000\pi h} = \pi {h^2} \Leftrightarrow h\; = \;\sqrt[3]{{\frac{{4000}}{\pi }}}
\end{array}\)
Sử dụng bảng biến thiên, ta tìm được Stp nhỏ nhất khi \(h\; = \;\sqrt[3]{{\frac{{4000}}{\pi }}}\)
.jpg.png)











