Số các giá trị nguyên của tham số m để phương trình \(\log _{\sqrt{2}}(x-1)=\log _{2}(m x-8)\) có hai nghiệm thực phân biệt là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\log _{\sqrt{2}}(x-1)=\log _{2}(m x-8) \Leftrightarrow\left\{\begin{array} { l } { x - 1 > 0 } \\ { m x - 8 > 0 } \\ { ( x - 1 ) ^ { 2 } = m x - 8 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { x > 1 } \\ { ( x - 1 ) ^ { 2 } = m x - 8 } \end{array} \Leftrightarrow \left\{\begin{array}{l} x>1 \\ m=\frac{x^{2}-2 x+9}{x} \end{array}\right.\right.\right.\)
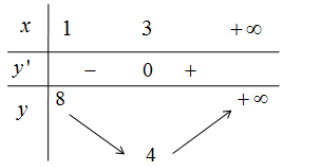
\(\begin{aligned} &\text { Xét hàm số } y=\frac{x^{2}-2 x+9}{x} \text { trên }(1 ;+\infty) \text { , ta có } y^{\prime}=\frac{x^{2}-9}{x^{2}} \text { . Giải } y^{\prime}=0 \Leftrightarrow x=\pm 3\\ &\text { Bảng biến thiên } \end{aligned}\)
\(\text { Để thỏa mãn yêu cầu thì } 4<m<8 \text { nên các giá trị nguyên của tham số } m \text { là } 5,6,7 \text { . }\)