Trắc nghiệm Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán Lớp 12
-
Câu 1:
Hàm số \(y=\cos 2 x-4 \sin x+4\) có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \(\left[0 ; \frac{\pi}{2}\right]\) lần lượt là:
-
Câu 2:
Hàm số \(y=\cos 2 x+2 \sin x\) có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \(\left[0 ; \frac{\pi}{2}\right]\) lần lượt là \(y_{1} ; y_{2}\) Khi đó tích \(y_{1} . y_{2}\) có giá trị bằng:
-
Câu 3:
Hàm số \(y=\cos ^{2} x-2 \cos x-1\) có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn \([0 ; \pi]\)lần lượt bằng \(y_{1} ; y_{2}\) . Khi đó tích \(y_{1} . y_{2}\) có giá trị bằng:
-
Câu 4:
Hàm số \(y=\sqrt{3} \sin x+\cos x\) có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là:
-
Câu 5:
Hàm số \(y=-9 \sin x-\sin 3 x\) có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn\([0 ; \pi]\) lần lượt là
-
Câu 6:
Hàm số \(y=\sin ^{2} x+2\) có giá trị nhỏ nhất, giá trị lớn nhất lần lượt bằng
-
Câu 7:
Hàm số \(y=3 \sin x-4 \sin ^{3} x\) có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là:
-
Câu 8:
Hàm số \(y=\sin x+\cos x\) có giá trị nhỏ nhất, giá trị lớn nhất lần lượt là:
-
Câu 9:
Hàm số \(y=\tan x+x\) đạt giá trị nhỏ nhất trên đoạn \(\left[0 ; \frac{\pi}{4}\right]\) tại điểm có hoành độ bằng:
-
Câu 10:
Hàm số \(y=\cos 2 x-3\) đạt giá trị nhỏ nhất trên đoạn \([0 ; \pi]\) bằng:
-
Câu 11:
Hàm số \(y=\sin x+1\)đạt giá trị lớn nhất trên đoạn \(\left[-\frac{\pi}{2} ; \frac{\pi}{2}\right]\) bằng:
-
Câu 12:
Giá trị nhỏ nhất của hàm số \(y=5 \cos x-\cos 5 x \text { với } x \in\left[-\frac{\pi}{4} ; \frac{\pi}{4}\right]\) là:
-
Câu 13:
Giá trị nhỏ nhất của hàm số \(y=\sqrt{2} \cos 2 x+4 \sin x \text { trên }\left[0 ; \frac{\pi}{2}\right]\) là:
-
Câu 14:
Giá trị lớn nhất của hàm số \(y=2 \sin x-\frac{4}{3} \sin ^{3} x \text { trên }[0 ; \pi]\) là:
-
Câu 15:
Hàm số \(y=\sqrt{x^{2}+1}+x^{2}\) có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1;1] lần lượt là:
-
Câu 16:
Hàm số \(y=\frac{x-1}{\sqrt{x^{2}+2}}\) đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [-3;0] lần lượt tại \(x_{1} ; x_{2}\) Khi đó \(x_{1} . x_{2}\) bằng:
-
Câu 17:
Giá trị nhỏ nhất của hàm số \(y=\frac{\ln x}{x}\) trên đoạn [1;e] bằng là:
-
Câu 18:
Hàm số \(y=(x-1)^{2}+(x+3)^{2}\) có giá trị nhỏ nhất bằng:
-
Câu 19:
Hàm số \(y=\sqrt{4-x^{2}}\) đạt giá trị nhỏ nhất tại x. Giá trị của x là:
-
Câu 20:
Hàm số \(y=\frac{1}{3} x^{3}-\frac{5}{2} x^{2}+6 x+1\) đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [1;3] tại điểm có hoành độ lần lượt là \(x_{1} ; x_{2}\) . Khi đó tổng \(x_{1} +x_{2}\) bằng
-
Câu 21:
Hàm số \(y=x^{2}+2 x+1\) có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [0;1] lần lượt là \(y_{1} ; y_{2}\) Khi đó tích \(y_{1} . y_{2}\) bằng:
-
Câu 22:
Cho hàm số \(y=\frac{x^{2}-3}{x-2}\). Khẳng định nào sau đây đúng về giá trị lớn nhất và nhỏ nhất của hàm
số trên đoạn [3;4]:
-
Câu 23:
Giá trị lớn nhất của hàm số \(y=\frac{x-1}{x+2}\) trên đoạn [0;2] là:
-
Câu 24:
Hàm số \(y=x^{4}-2 x^{2}+1\) có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [0;2] lần lượt là:
-
Câu 25:
Giá trị lớn nhất của hàm số \(y=\frac{1}{3} x^{3}-2 x^{2}+3 x-4\) trên đoạn [1;5] là:
-
Câu 26:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{5-4 x}\) trên đoạn [-1;1] là:
-
Câu 27:
Giá trị lớn nhất của hàm số \(y=\frac{x^{2}-8 x+7}{x^{2}+1}\) là:
-
Câu 28:
Giá trị nhỏ nhất của hàm số \(f(x)=\frac{x^{2}-x+1}{x-1}\) trên khoảng \((1 ;+\infty)\) là:
-
Câu 29:
Giá trị nhỏ nhất của hàm số \(y=x+\frac{9}{x}\) trên đoạn [2;4] là:
-
Câu 30:
Giá trị nhỏ nhất của hàm số \(y=\frac{x-1}{x+1}\) trên đoạn [0;3] là:
-
Câu 31:
Giá trị nhỏ nhất của hàm số \(y=x(x+2)(x+4)(x+6)+5\) trên nữa khoảng \([-4 ;+\infty)\) là:
-
Câu 32:
Giá trị lớn nhất của hàm số \(f(x)=x^{4}-2 x^{2}+1\) trên đoạn [0;2] là:
-
Câu 33:
Giá trị lớn nhất của hàm số \(f(x)=x^{3}-8 x^{2}+16 x-9\) trên đoạn [1;3] là:
-
Câu 34:
Giá trị nhỏ nhất của hàm số \(f(x)=x^{3}-3 x^{2}-9 x+3\) trên đoạn [-4;4] là:
-
Câu 35:
Giá trị nhỏ nhất của hàm số \(y=x^{3}-3 x+5\) trên đoạn [0;2] là:
-
Câu 36:
Tìm m để hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaamyBaiaa % dIhacqGHRaWkcaaI1aaabaGaamiEaiabgkHiTiaad2gaaaaaaa!40E7! f\left( x \right) = \frac{{mx + 5}}{{x - m}}\) đạt giá trị nhỏ nhất trên đoạn [0;1] bằng -7.
-
Câu 37:
Cho 2 số thực không âm x;y thỏa mãn x + y =1. Giá trị lớn nhất của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiabg2 % da9maalaaabaGaamiEaaqaaiaadMhacqGHRaWkcaaIXaaaaiabgUca % RmaalaaabaGaamyEaaqaaiaadIhacqGHRaWkcaaIXaaaaaaa!4004! S = \frac{x}{{y + 1}} + \frac{y}{{x + 1}}\) là :
-
Câu 38:
Tìm giá trị nhỏ nhất m của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkdaWcaaqaaiaa % ikdaaeaacaWG4baaaiaacYcacaWG4bGaeyOpa4JaaGimaiaac6caaa % a!40B4! y = {x^2} + \frac{2}{x},x > 0\).
-
Câu 39:
Cho hàm số y=f(x) có đạo hàm và liên tục trên R. Biết đồ thị hàm số y=f′(x) như hình vẽ dưới. Xét hàm số \(g(x)=f^2(x)–3f(x)\). Biết\( f(2)=1, f(0)=–2, f(–1)=–3, f(3)=–1\), \(\mathop {\lim }\limits_{x \to \pm \infty } f(x) = - \infty \). Mệnh đề nào sau đây đúng?
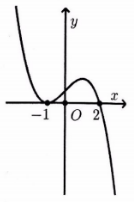
-
Câu 40:
Cho hàm số y = f ( x) có đồ thị như hình bên. Tìm giá trị lớn nhất của hàm số y = f ( x) trên đoạn [-1;2]
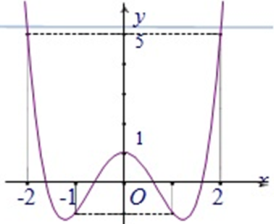
-
Câu 41:
Tìm giá trị nhỏ nhất của hàm số \(y=\frac{x^2-4x}{2x+1}\)trên đoạn [0;3]
-
Câu 42:
Gia trị lớn nhất của hàm số \(y=\frac{x^2+3x+3}{x+1}\) trên đoạn \(\left[ { - \frac{1}{2};1} \right]\)
-
Câu 43:
Tìm giá trị nhỏ nhất của hàm số \(y=\frac{x^2+3}{x-1}\)trên đoạn [2;4] .
-
Câu 44:
Tìm giá trị nhỏ nhất của hàm số \(y=\frac{x^2-5}{x+3}\)trên đoạn [0;2]
-
Câu 45:
Giá trị nhỏ nhất của hàm số \(y=2x+1+\frac{1}{2x+1}\)trên đoạn [1; 2] bằng
-
Câu 46:
Tính giá trị nhỏ nhất của hàm số \(y=x+\frac{4}{x+1}\)trên đoạn [0; 4]
-
Câu 47:
Cho hàm số \(y=x+\frac{1}{x+2}\), giá trị nhỏ nhất m của hàm số trên [-1, 2] là:
-
Câu 48:
Giá trị nhỏ nhất của hàm số \(y=\frac{2x+1}{1-x}\)trên đoạn [2;3] bằng:
-
Câu 49:
Cho hàm số \(y=\frac{x+1}{2x-1}\). Chọn phương án đúng trong các phương án sau
-
Câu 50:
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=\frac{x-1}{2x+1}\)trên đoạn [1;3] là:











