Trắc nghiệm Tích phân Toán Lớp 12
-
Câu 1:
Tính tích phân \(I = \mathop \smallint \nolimits_0^4 \frac{{2{x^2} + 4x + 1}}{{\sqrt {2x + 1} }}dx\)
-
Câu 2:
Tính tích phân \(I = \mathop \smallint \nolimits_{ - 2}^2 \left| {x + 1} \right|dx\)
-
Câu 3:
Tính tích phân \(\mathop \smallint \nolimits_{\frac{{\rm{\pi }}}{4}}^{\frac{{3{\rm{\pi }}}}{4}} \left| {\sin 2x} \right|dx\) ta được kết quả :
-
Câu 4:
Tính tích phân sau \(\mathop \smallint \nolimits_{ - \frac{{\rm{\pi }}}{2}}^{\frac{{\rm{\pi }}}{3}} \left| {\sin x} \right|dx\)
-
Câu 5:
Tính tích phân sau: \(\mathop \smallint \nolimits_0^2 \left| {{x^2} - 1} \right|dx\)
-
Câu 6:
Tính tích phân sau \(J = \mathop \smallint \nolimits_2^7 \frac{{xdx}}{{\sqrt {x + 2} + \sqrt {x - 2} }}\)
-
Câu 7:
Tính tích phân sau: \(I = \mathop \smallint \nolimits_0^1 \frac{{xdx}}{{\sqrt {3x + 1} + \sqrt {2x + 1} }}\)
-
Câu 8:
Cho hàm số f(x) liên tục trên đoạn [0; 10] thỏa mãn \(\mathop \smallint \nolimits_0^{10} f\left( x \right)dx = 7,\mathop \smallint \nolimits_2^6 f\left( x \right)dx = 3\). Tính \(P = \mathop \smallint \nolimits_0^2 f\left( x \right)dx + \mathop \smallint \nolimits_6^{10} f\left( x \right)dx\)
-
Câu 9:
Cho \(\mathop \smallint \nolimits_1^3 f\left( x \right)dx = - 5,\;\mathop \smallint \nolimits_1^3 \left[ {f\left( x \right) - 2g\left( x \right)} \right]dx = 9.\). Tính \(I = \mathop \smallint \nolimits_1^3 g\left( x \right)dx\)
-
Câu 10:
Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính \(I = \int\limits_{ - 1}^2 {\left[ {f\left( x \right) + 2x} \right]dx} \), biết F(-1) = 1, F(2) = 4.
-
Câu 11:
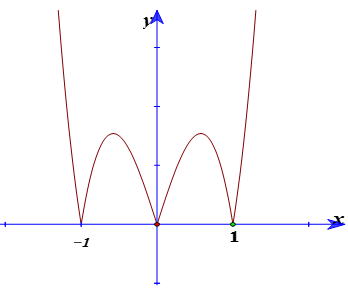
Cho hàm số y = f( x) = ax4+ bx2+ c (a > 0) có đồ thị (C), đồ thị hàm số y = f’(x). Đồ thị hàm số y = f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
-
Câu 12:
Cho hàm số y = f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = -9 tại điểm có hoành độ dương và đồ thị hàm số y = f’ (x) cho bởi hình vẽ bên. Tìm phần nguyên của giá trị diện tích hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
-
Câu 13:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = e2x, trục hoành và hai đường thẳng x = 0 ; x = 3 là
-
Câu 14:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = tanx , trục hoành và hai đường thẳng \(x = \frac{{\rm{\pi }}}{6};\;x = \;\frac{{\rm{\pi }}}{4}\) là
-
Câu 15:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = sin x , trục hoành và hai đường thẳng \[x = {\rm{\pi }}\;;\;{\rm{x}} = \frac{{3{\rm{\pi }}}}{2}\) là
-
Câu 16:
Cho hình phẳng (D) giới hạn bởi các đường y = \({\left( {x - 2} \right)^2}\) và y = 4. Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Ox
-
Câu 17:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = \(\sqrt[3]{x}\), trục hoành và hai đường thẳng x =1 ; x = 8 là
-
Câu 18:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = \(\sqrt x \), trục hoành và hai đường thẳng x = 1 ; x = 4 là
-
Câu 19:
Tính diện tích hình phẳng D giới hạn bởi các đường \(y = {\sin ^2}x\cos x,x = 0,x = \pi ,y = 0\)
-
Câu 20:
Tính diện tích hình phẳng giới hạn bởi : Đồ thị hàm số y = x3 - 4x , trục hoành, đường thẳng x = 2 và đường thẳng x = 4.
-
Câu 21:
Tính diện tích hình phẳng giới hạn bởi : Đồ thị hàm số y = ex +1 , trục hoành , đường thẳng x = 0 và đường thẳng x = 1
-
Câu 22:
Tính diện tích hình phẳng giới hạn bởi : Đồ thị hàm số y = x + x−1, trục hoành , đường thẳng x = 1 và x = 2
-
Câu 23:
Tính diện tích hình phẳng giới hạn bởi: Đồ thị hàm số y = x3, trục hoành và hai đường thẳng x = -2, x = 2
-
Câu 24:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = x3, trục hoành và hai đường thẳng x = 1; x = 3 là
-
Câu 25:
Cho hình phẳng (D) giới hạn bởi các đường \(y = {\left( {x - 2} \right)^2}\) và y = 4. Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Oy
-
Câu 26:
Tính \(I = \mathop \smallint \nolimits_{ - \frac{1}{2}}^3 \frac{{xdx}}{{\sqrt[3]{{2x + 2}}}}\)
-
Câu 27:
Tính \(J = \mathop \smallint \nolimits_2^3 \frac{{2x + 3}}{{{x^3} - 3x + 2}}dx\)
-
Câu 28:
Tính tích phân \(I = \mathop \smallint \nolimits_3^4 \frac{{{x^2}dx}}{{{x^2} - 3x + 2}}\)
-
Câu 29:
Tính tích phân \(J = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{4}} {\cos ^4}2xdx\)
-
Câu 30:
Tính tích phân \(I = \mathop \smallint \nolimits_{ - \frac{{\rm{\pi }}}{2}}^{\frac{{\rm{\pi }}}{2}} \sin 2x.\sin 3xdx\)
-
Câu 31:
Tính tích phân \(I = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} {\sin ^2}x{\cos ^3}xdx\)
-
Câu 32:
Tính tích phân \(I = \mathop \smallint \nolimits_0^{\rm{\pi }} {\sin ^2}x.{\cos ^2}xdx\)
-
Câu 33:
Tính tích phân sau \(I = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} x\;\cos \;xdx\)
-
Câu 34:
Tính tích phân sau \(I = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{4}} \left( {2x + 3} \right).\sin \;4xdx\)
-
Câu 35:
Tính tích phân sau \(I = \mathop \smallint \nolimits_0^{e - 1} x\ln \left( {x + 1} \right)dx\)
-
Câu 36:
Tính tích phân sau \(I = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} x\;\sin xdx\)
-
Câu 37:
Tính \(C = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} {x^2}\cos xdx\)
-
Câu 38:
Tính \(\mathop \smallint \nolimits_0^1 x.{e^{2x}}dx\)
-
Câu 39:
Tính tích phân sau: \(A = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{4}} \frac{{xdx}}{{{{\cos }^2}x}}\)
-
Câu 40:
Tính tích phân \(\mathop \smallint \nolimits_0^1 x.{e^x}dx\)
-
Câu 41:
Tính tích phân sau: \(I = \mathop \smallint \nolimits_0^1 \frac{{dx}}{{1 + {x^2}}}\)
-
Câu 42:
Tính tích phân sau: \(I = \mathop \smallint \nolimits_0^1 \sqrt {1 - {x^2}} dx\)
-
Câu 43:
Tính tích phân sau: \(I = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} {\sin ^5}xdx\)
-
Câu 44:
Tính tích phân sau: \(I = \mathop \smallint \nolimits_{\ln 2}^{\ln 5} \frac{{{e^{2x}}dx}}{{\sqrt {{e^x} - 1} }}\)
-
Câu 45:
Tính tích phân sau \(J = \mathop \smallint \nolimits_{\sqrt 5 }^{2\sqrt 3 } \frac{{dx}}{{x\sqrt {{x^2} + 4} }}\)
-
Câu 46:
Tính tích phân sau: \(I = \mathop \smallint \nolimits_{\sqrt 3 }^{2\sqrt 2 } \frac{{\sqrt {1 + {x^2}} }}{x}dx\)
-
Câu 47:
Tính tích phân sau: \(\mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} \sin \;3x.\cos \;xdx\)
-
Câu 48:
Tính tích phân sau \(\mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} \left( {2\cos \;x - \sin \;2x} \right)dx\)
-
Câu 49:
Tìm mệnh đề đúng trong các mệnh đề sau:
-
Câu 50:
Biết \(\mathop \smallint \nolimits_0^1 \frac{{x + 2}}{{{x^2} + 4x + 7}}dx = a\ln \sqrt {12} + b\ln \sqrt 7 \), với a, b là các số nguyên. Tổng a + b là :











