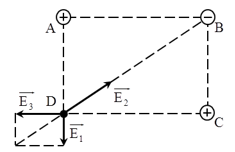
Bốn điểm A, B, C và D trong không khí tạo thành một hình chữ nhật ABCD với AD = a = 3 cm, AB = b = 4 cm. Các điện tích q1, q2 và q3 lần lượt đặt tại A, B và C. Biết q2=−12,5.10−8 C và cường độ điện trường tổng hợp tại D bằng 0. Tính q1 và q3
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai+ Véctơ cường độ điện trường tại D:
\( \overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \)
Theo giả thuyết \( \overrightarrow {{E_D}} = 0 \to \overrightarrow {{E_2}} = - (\overrightarrow {{E_1}} + \overrightarrow {{E_3}} ) = - \overrightarrow {{E_{13}}} (*)\)
Mà q2 < 0 nên \( \overrightarrow {{E_2}} \nearrow \nearrow \overrightarrow {DB} \)
Do vậy \( \overrightarrow {{E_1}} ; \overrightarrow {{E_3}} \) hướng ra xa q1 và q3 \(\to \) \(q_1 > 0; q_3 > 0.\)
+ Chiếu (*) lên phương DC, chiều dương từ D đến C ta được: \(\begin{array}{l} {E_2}\cos \widehat {BDC} = {E_3} \to {E_3} = {E_2}.\frac{{DC}}{{\sqrt {D{C^2} + B{C^2}} }} = {E_2}\frac{4}{5}\\ \to k\frac{{\left| {{q_3}} \right|}}{{D{C^2}}} = k\frac{{\left| {{q_2}} \right|}}{{B{D^2}}}.\frac{4}{5} \Leftrightarrow \left| {{q_3}} \right| = \left| {{q_2}} \right|\frac{{D{C^2}}}{{B{D^2}}}.\frac{4}{5} = \left| {{q_2}} \right|.\frac{{{4^2}}}{{{5^2}}} \end{array}\)
Vì q3 > 0 nên \(q_3 = 6,4.10^{-8} C.\)
+ Chiếu (*) lên phương AD, chiều dương từ D đến A ta được: \(\begin{array}{l} {E_2}\sin \widehat {BDC} = {E_1} \to {E_1} = {E_2}.\frac{{BC}}{{\sqrt {D{C^2} + B{C^2}} }} = {E_2}\frac{3}{5}\\ \to k\frac{{\left| {{q_1}} \right|}}{{A{D^2}}} = k\frac{{\left| {{q_2}} \right|}}{{B{D^2}}}.\frac{3}{5} \Leftrightarrow \left| {{q_1}} \right| = \left| {{q_2}} \right|\frac{{A{D^2}}}{{B{D^2}}}.\frac{3}{5} = \left| {{q_2}} \right|.\frac{{{3^2}}}{{{5^2}}} \end{array}\)
Vì q1 > 0 nên q1 = 2,7.10-8 C.