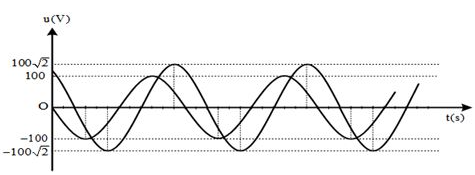
Cho đoạn mạch xoay chiều với \(R=100\text{ }\Omega ,\text{ }C=0,{{318.10}^{-4}}\text{ }F.\) Điện áp giữa hai đầu mạch \({{u}_{AB}}=200\sqrt{2}\sin \left( 100\pi t+\frac{\pi }{4} \right)\text{ V,}\) cuộn cảm thuần giá trị L = 0,636 H. Biểu thức của cường độ qua mạch là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiCảm kháng và dung kháng của mạch:
\({{Z}_{L}}=\omega L=200\text{ }\Omega ;\text{ }{{Z}_{C}}=\frac{1}{\omega C}=100\text{ }\Omega .\)
Độ lệch pha giữa u và i:
\(\tan \Delta \varphi =\tan \left( {{\varphi }_{u}}-{{\varphi }_{i}} \right)=\frac{{{Z}_{L}}-{{Z}_{C}}}{R}=1\Rightarrow {{\varphi }_{u}}-{{\varphi }_{i}}=\frac{\pi }{4}\Rightarrow {{\varphi }_{i}}=\frac{\pi }{4}-\frac{\pi }{4}=0.\)
Cường độ dòng điện cực đại của đoạn mạch:
\({{I}_{0}}=\frac{{{U}_{0}}}{Z}=\frac{{{U}_{0}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{200\sqrt{2}}{100\sqrt{2}}=2\text{ A}.\)
Biểu thức cường độ điện trường:
\(\text{i}=2\text{sin}\left( 100\pi \text{t} \right)\text{ }\left( A \right).\)
Câu hỏi liên quan
-
Đặt hiệu điện thế xoay chiều \(u=160\sqrt{2}cos100\pi t\text{ }\left( V \right)\) vào hai đầu một đoạn mạch xoay chiều thấy biểu thức dòng điện là \(i=\sqrt{2}\cos \left( 100\pi t+\frac{\pi }{2} \right)\text{ (A)}\text{.}\) Mạch này có những linh kiện gì ghép nối tiếp với nhau?
-
Trong mach điện xoay chiều R, L, C nối tiếp \(\omega\) là tần số góc, Z là tổng trở của đoạn mạch. Chọn hệ thức đúng:
-
Đặt một điện áp \(u={{U}_{0}}\cos \left( 100\pi t \right)\text{ }(V)\) (t tính bằng s) vào hai đầu đoạn mạch gồm một cuộn dây có độ tự cảm \(L=\frac{0,15}{\pi }\text{ }H\) và điện trở \(r=5\sqrt{3}\text{ }\Omega \) mắc nối tiếp với một tụ điện có điện dung \(C=\frac{{{10}^{-3}}}{\pi }\text{ }F.\) Tại thời điểm t1 điện áp tức thời hai đầu cuộn dây có giá trị 15 V, đến thời điểm \({{t}_{2}}=\left( {{t}_{1}}+\frac{1}{75} \right)\text{ }s\) thì điện áp tức thời hai đầu tụ điện cũng bằng 15 V. Giá trị của U0 bằng
-
Cho đoạn mạch xoay chiều RLC nối tiếp. Vôn kế mắc vào giữa hai đầu điện trở thuần R chỉ 20 V, giữa hai đầu cuộn cảm thuần L chỉ 55 V và giữa hai đầu tụ điện chỉ 40 V. Nếu mắc vôn kế vào giữa hai đầu đoạn mạch trên thì vôn kế sẽ chỉ
-
Cần ghép một tụ điện nối tiếp với các linh kiện khác theo cách nào dưới đây, để có được đoạn mạch xoay chiều mà dòng điện trễ pha \(\frac{\pi }{4}\) đối với điện áp giữa hai đầu đoạn mạch. Biết tụ điện trong mạch này có dung kháng bằng 20 Ω.
-
Chọn đáp án sai. Hiện tượng cộng hưởng trong mạch điện xoay chiều không phân nhánh RLC xảy ra khi
-
Hai cuộn dây (R1, L1) và (R2, L2) được mắc nối tiếp nhau và mắc vào một hiệu điện thế xoay chiều có giá trị hiệu dụng U. Gọi U1 và U2 là hiệu điện thế hiệu dụng tương ứng giữa hai đầu cuộn (R1, L1) và (R2, L2). Điều kiện để U = U1 + U2 là
-
Một đoạn mạch gồm cuộc dây thuần cảm có độ tự cảm \(\text{L}=\frac{\text{1}}{\pi }\text{ H}\) mắc nối tiếp với điện trở thuần R = 100 W. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u=100\sqrt{2}\cos \left( 100\pi t \right)\text{ (V)}\text{.}\) Biểu thức cường độ dòng điện trong mạch là
-
Dung kháng của một mạch RLC mắc nối tiếp đang có giá trị nhỏ hơn cảm kháng. Muốn xảy ra hiện tượng cộng hưởng điện trong mạch ta phải
-
Một bàn là 200 V – 1000 W được mắc vào điện áp xoay chiều \(u=100\sqrt{2}\cos \left( 100\pi t \right)\text{ }(V).\) Bàn là có độ tự cảm nhỏ không đáng kể. Dòng điện chạy qua bàn là có biểu thức nào?
-
Mạch điện (AB ) gồm đoạn (AM ) và đoạn (MB ): Đoạn (AM ) có một điện trở thuần (50ôm ) và đoạn (MB ) có một cuộn dây. Đặt vào mạch (AB ) một điện áp xoay chiều thì điện áp tức thời của hai đoạn (AM ) và (MB ) biến thiên như trên đồ thị: Cảm kháng của cuộn dây là:
-
Trong đoạn mạch R, L, C nối tiếp, đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng không đổi. Khi trong mạch xảy ra hiện tượng cộng hưởng thì kết luận nào sau đây không đúng?
A. B.
C. D.
-
Đặt điện áp xoay chiều vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Biết R = 10 Ω, cuộn cảm thuần có \(L=\frac{1}{10\pi }\text{ }H,\) tụ điện có \(C=\frac{{{10}^{-3}}}{2\pi }\text{ }F\) và điện áp giữa hai đầu cuộn cảm thuần là \({{u}_{L}}=20\sqrt{2}cos\left( 100\pi t+\frac{\pi }{3} \right)V.\) Biểu thức điện áp giữa hai đầu đoạn mạch là
-
Đặt một hiệu điện thế xoay chiều có giá trị hiệu dụng không đổi vào hai đầu đoạn mạch RLC không phân nhánh. Hiệu điện thế giữa hai đầu
-
Đặt điện áp xoay chiều u vào hai đầu đoạn mạch có R, L, C mắc nối tiếp thì dòng điện trong đoạn mạch có cường độ i. Hình bên là một phần đồ thị biểu diễn sự phụ thuộc của tích u.i theo thời gian t. Hệ số công suất của đoạn mạch là:
-
Nếu đặt vào hai đầu một mạch điện chứa một điện trở thuần R và một tụ điện C mắc nối tiếp một điện áp xoay chiều có biểu thức \(u={{U}_{0}}\cos \left( \omega t-\frac{\pi }{2} \right)\text{ }(V).\) Khi đó dòng điện trong mạch có biểu thức \(i={{I}_{0}}\cos \left( \omega t-\frac{\pi }{4} \right)\text{ }(A).\) Biểu thức điện áp giữa hai bản tụ sẽ là:
-
Cho mạch điện RLC gồm \(R=40\text{ }\Omega ,\text{ }L=\frac{0,3}{\pi }\text{ }H,\text{ }C=\frac{{{10}^{-3}}}{7\pi }\text{ }F.\) Đặt vào hai đầu đoạn mạch điện áp \(u=200\cos \left( 100\pi t+\frac{\pi }{8} \right)\text{ V}\text{.}\) Pha ban đầu của cường độ dòng điện là
-
Cho mạch điện xoay chiều R, L, C. Khi chỉ nối R, C vào nguồn điện thì thấy i sớm pha \(\frac{\pi }{4}\) so với điện áp trong mạch. Khi mắc cả R, L, C nối tiếp vào mạch thì thấy i chậm pha \(\frac{\pi }{4}\) so với điện áp hai đầu đoạn mạch. Xác định liên hệ ZL theo ZC.
-
Đoạn mạch RLC nối tiếp. Biết điện áp tức thời ở hai đầu đoạn mạch sớm pha hơn cường độ dòng điện tức thời i chạy qua mạch 450. Chọn kết luận đúng:
-
Đặt điện áp xoay chiều vào hai đầu đoạn mạch X mắc nối tiếp chứa hai trong ba phần tử: điện trở thuần, cuộn cảm thuần và tụ điện. Biết rằng điện áp giữa hai đầu đoạn mạch X luôn sớm pha so với cường dộ dòng điện trong mạch một góc nhỏ hơn \(\frac{\pi }{2}.\) Đoạn mạch X chứa
