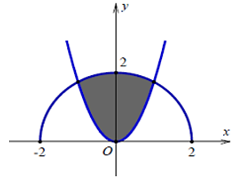
Cho (H) là hình phẳng giới hạn bởi parabol \(y=\sqrt 3 {x^2}\) và nửa đường tròn có phương trình \(y=\sqrt {4\; - {x^2}} \) với −2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng

Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x² , y = 4x - 4 và y = -4x - 4

Cho hàm số f liên tục trên \(\mathbb{R}\) . Nếu\(\begin{aligned} &\int_{1}^{5} 2 f(x) d x=2 \text { và } \int_{1}^{3} f(x) d x=7 \text { thì } \int_{3}^{5} f(x) d x \end{aligned}\) có giá trị
bằng:
 

Tính \(\int_{0}^{\pi} x(1+\cos x) d x\) kết quả là:

Cho hàm số\(y=x^{4}-3 x^{2}+m\) có đồ thị (Cm ) , với m là tham số thực. Giả sử (Cm ) cắt trục Ox tại bốn điểm phân biệt như hình vẽ

Gọi \(S_{1}, S_{2}, S_{3}\) là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để \(S_{1}+S_{3}=S_{2}\)

Cho hàm số f(x) liên tục trên \(\mathbb{R}\) , có đồ thị như hình vẽ. Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hàm số f(x ) , trục hoành và trục tung. Khẳng định nào sau đây đúng?

\(\text { Đặt } I=\int_{1}^{2}(2 m x+1) \mathrm{d} x\)  ( là tham số thực). Tìm  để I=4

Nếu \(\int_{0}^{1}[3 f(x)+x] \mathrm{d} x=2 \text{ thì } \int_{0}^{1} f(x) \mathrm{d} x\) bằng:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(f’\left( x \right) \in \left[ { – 1;1} \right]\) với mọi \(x \in \left[ {0;2} \right]\). Biết rằng \(f\left( 0 \right) = f\left( 2 \right) = 1\). Đặt \(I = \int\limits_0^2 {f\left( x \right){\rm{d}}x} \), phát biểu nào dưới đây đúng?

Để tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamytaiabg2 % da9maapehabaWaaeWaaeaacaWG4bGaey4kaSIaaGymaaGaayjkaiaa % wMcaaiaaikdadaahaaWcbeqaaiaadIhaaaaabaGaaGimaaqaaiaaig % daa0Gaey4kIipaaaa!41A8! M = \int\limits_0^1 {\left( {x + 1} \right){2^x}} \) bằng phương pháp tích phân từng phần ta đặt u = x + 1 và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaeizaabaaa % aaaaaapeGaamODaiabg2da9iaaikdadaahaaWcbeqaaiaadIhaaaGc % caWGKbGaamiEaaaa!3CD2! {\rm{d}}v = {2^x}dx\). Tìm du và tính M

Tích phân \(I=\int_{1}^{2} \frac{x^{2}}{x^{2}-7 x+12} d x\) có giá trị bằng
 

Tích phân \(I=\int_{-1}^{1}\left(a x^{3}+\frac{b}{x+2}\right) d x\) có giá trị là

Diện tích hình phẳng giới hạn bởi các đường cong \(y=\sin x, y=\cos x\) và các đường thẳng x = 0 , x = π bằng ?

Tích phân \(I=\int_{-1}^{1} \frac{x}{\sqrt{x+1}-1} d x\) có giá trị là
 

Tích phân \(\int_{0}^{3} x(x-1) d x\) có giá trị bằng với giá trị của tích phân nào trong các tích phân dưới đây?

Cho hình phẳng giới hạn bởi đường cong \(y=\tan x\) , trục hoành và hai đường thẳng \(x=0, x=a \text { với } a \in\left(0 ; \frac{\pi}{2}\right)\) Thể tích khối tròn xoay thu được khi quay hình phẳng này xung quanh trục

\(\begin{equation} \text { Nếu } \int_{1}^{2} f(x) d x=3 \end{equation}\) \(\begin{equation} \text { và } \int_{1}^{2} g(x) d x=-1 \text { thì } \int_{1}^{2}[2 f(x)+3 g(x)] d x \text { bằng } \end{equation}\)

Cho hàm số \(y = f\left( x \right)\) là hàm số chẵn, liên tục trên đoạn \(\left[ { – \pi ;\pi } \right]\), thỏa mãn \(\int_0^\pi {f\left( x \right){\rm{d}}x} = 2\). Giá trị tích phân \(I = \int_{ – \pi }^\pi {\frac{{f\left( x \right)}}{{{{2020}^x} + 1}}{\rm{d}}x} \) bằng?

Tích phân \(\int\limits_1^2 {2x{\rm{d}}x} \) có giá trị là:

Tích phân \(I=\int_{-2}^{-1}\left(2 a x^{3}+\frac{1}{x}\right) d x\) có giá trị là

Tích phân \(\int_{0}^{\frac{\pi}{4}} \frac{x}{1+\cos 2 x} \mathrm{d} x=a \pi+b \ln 2, \text { với } a, b\) là các số thực. Tính 16a-8b