Cho hàm số f(x) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên dưới.
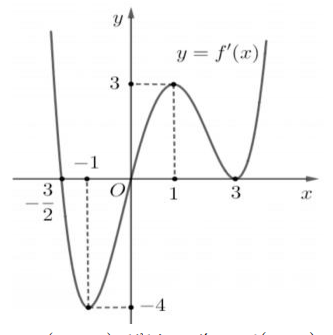
Có bao nhiêu số nguyên \(m\in (-10;10)\) để hàm số \(y=f(3 x-1)+x^{3}-3 m x\) đồng biến trên khoảng (-2;1) .
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(y^{\prime}=3 f^{\prime}(3 x-1)+3 x^{2}-3 m\)
Hàm số dồng biến trên (-2;1) khi \(y^{\prime}=3 f^{\prime}(3 x-1)+3 x^{2}-3 m \geq 0 \quad \forall x \in(-2 ; 1)\)
\(\Leftrightarrow f^{\prime}(3 x-1)+x^{2}-m \geq 0 \forall x \in(-2 ; 1) \Rightarrow m \leq g(x)=f^{\prime}(3 x-1)+x^{2}, \forall x \in(-2 ; 1)\,\,\,(*)\)
Ta có \(f^{\prime}(3 x-1) \geq f^{\prime}(-1)=-4, x^{2} \geq 0 \Rightarrow f^{\prime}(3 x-1)+x^{2} \geq-4\)
Suy ra (*) \(\Leftrightarrow m \leq \operatorname{Min}_{(-2 ; 1)} g(x)=-4 \Rightarrow m=\{-9 ;-8 ;-7 ;-6 ;-5 ;-4\}\)
Vậy có 6 giá trị nguyên thỏa mãn điều kiện đề bài
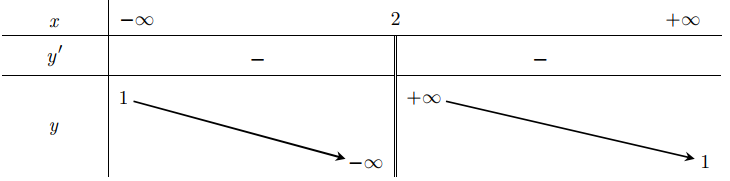
.png)
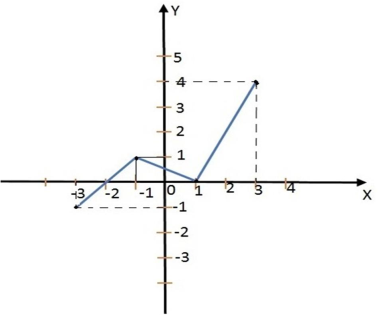
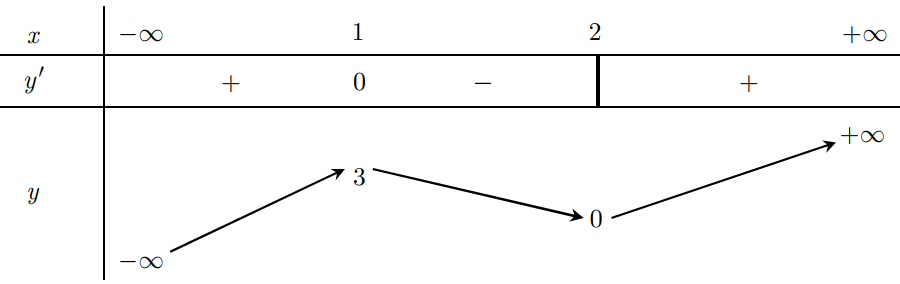
.png)












