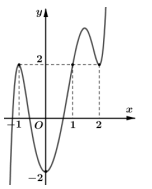
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên và \(f\left( 0 \right) = 0;f\left( 4 \right) > 4\). Biết hàm \(y = f’\left( x \right)\) có đồ thị như hình vẽ bên. Tìm số điểm cực trị của hàm số \(g\left( x \right) = \left| {f\left( {{x^2}} \right) – 2x} \right|\).
.jpg.png)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(h\left( x \right) = f\left( {{x^2}} \right) – 2x\). Ta có \(h’\left( x \right) = 2x.f’\left( {{x^2}} \right) – 2\).
Từ đồ thị ta thấy \(f’\left( {{x^2}} \right) \ge 0,\forall x\). Do đó \(h’\left( x \right) < 0,\forall x < 0\).
Với x > 0, ta có \(h’\left( x \right) = 0 \Leftrightarrow f’\left( {{x^2}} \right) = \frac{1}{x}\).
Đặt \(t = {x^2}\), phương trình trở thành \(f’\left( t \right) = \frac{1}{{\sqrt t }} \Leftrightarrow t = {t_0} \in \left( {0;1} \right)\). Khi đó \(h’\left( x \right) = 0 \Leftrightarrow x = \sqrt {{t_0}} \)
.jpg.png)
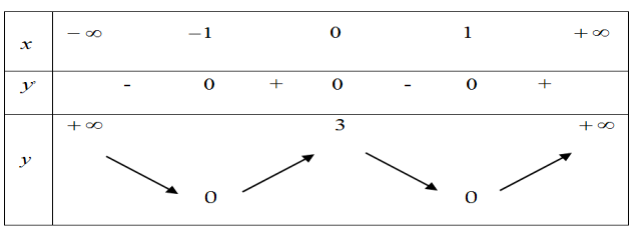
Ta có \(h\left( 0 \right) = f\left( 0 \right) = 0\) và \(h\left( 2 \right) = f\left( 4 \right) – 4 > 0\).
Bảng biến thiên
.png)
Từ bảng biến thiên ta có hàm số \(y = h\left( x \right)\) có 1 điểm cực trị và đồ thị hàm số \(y = h\left( x \right)\) cắt Ox tại 2 điểm phân biệt \( \Rightarrow \) Hàm số \(y = g\left( x \right) = \left| {h\left( x \right)} \right|\) có ba điểm cực trị.
Câu hỏi liên quan
-
Hàm số y=f(x) có \(f'\left( x \right) = \left( {x + 1} \right){\left( {x + 2} \right)^2}{\left( {x + 3} \right)^4}{\left( {x + 4} \right)^3}\). Số điểm cực trị của hàm số là:
-
Nhân ngày phụ nữ Việt Nam 20 -10 - 2021 , ông A quyết định mua tặng vợ một món quà và đặt nó vào trong một chiếc hộp có thể tích là 32 (đvtt) có đáy hình vuông và không có nắp . Để món quà trở nên thật đặc biệt và xứng đáng với giá trị của nó ông quyết định mạ vàng cho chiếc hộp , biết rằng độ dạy lớp mạ tại mọi điểm trên hộp là như nhau . Gọi chiều cao và cạnh đáy của chiếc hộp lần lượt là h; x. Để lượng vàng trên hộp là nhỏ nhất thì giá trị của h; x phải là ?
-
Giá trị cực tiểu của hàm số \(y = {x^4} - 2{x^2} + 5\) là
-
Số điểm cực tiểu của hàm số \(f\left( x \right) = \frac{1}{5}{{\rm{x}}^4} - \frac{4}{3}{{\rm{x}}^2} + 2\) là
-
Biết hàm số f(x) xác định trên R và có đạo hàm f’(x) = (x – 1)x2(x + 1)3(x + 2)4. Hỏi hàm số có bao nhiêu điểm cực trị?
-
Cho hàm số y = f (x) có bảng biến thiên như sau:
Mênh đề nào dưới đây đúng?
-
Cho hàm số \(y = {x^4} – 2m{x^2} + m\). Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
-
Điểm cực đại của đồ thị hàm số \(y = 2{x^3} – 3{x^2} – 2\) là.
-
Đồ thị hàm số \(y = {x^4} - 3{x^2} + 5\) có bao nhiêu điểm cực tiểu?
-
Cho hàm số y = f ( x) có đạo hàm \(f '( x) = x (x² + 2x)^3 (x² -\sqrt 2 )\,\,\forall x\in\mathbb{R}\) . Số điểm cực trị của hàm số là
-
Cho hàm số y=f(x) có \(f'\left( x \right) = \frac{1}{2}{x^3}{\left( {x - 1} \right)^2}\left( {2x - 1} \right){\left( {x + 2} \right)^5}\). Điểm cực tiểu của hàm số là
-
Cho hàm số y=f(x) có đồ thị như hình bên dưới. Đồ thị hàm số \(g(x)=f(|x|-2)\) có bao nhiêu điểm cực trị ?
-
Số điểm cực đại của hàm số \(f\left( x \right) = \frac{1}{3}{{\rm{x}}^4} + {{\rm{x}}^2} + 7\) là
-
Điểm cực tiểu của hàm số \(y = \frac{1}{4}{x^4} + 2{x^2} - 2\) là:
-
Đường dây điện 110KV kéo từ trạm phát (điểm A) trong đất liền ra Côn Đảo (điểm C). biết khoảng cách ngắn nhất từ C đến B là 60km, khoảng cách từ A đến B là 100km, mỗi km dây điện dưới nước chi phí là 5000 USD, chi phí cho mỗi km dây điện trên bờ là 3000 USD. Hỏi điểm G cách A bao nhiêu để mắc dây điện từ A đến G rồi từ G đến C chi phí ít nhất.
-
Số điểm cực trị của hàm số \(y = {\left( {x – 1} \right)^{2023}}\) là
-
Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số \(y = {x^3} - 3x\) là
-
Một ngọn hải đăng đặt tại vị trí A có khoảng cách đến bờ biển AB=5km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng 7km. Người canh hải đăng có thể chèo đò từ A đến M trên bờ biển với vận tốc 4km/h rồi đi bộ đến C với vận tốc 6km/h. Vị trí của điểm M cách B một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
-
Hàm số nào sau đây không có cực trị?
-
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số \(y = {x^4} - 2m{x^2}\) có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.
