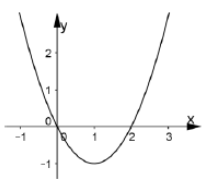
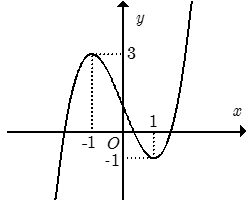
Cho hàm số y= f(x) = ax3+ bx2+cx+d có đạo hàm là hàm số y = f’ (x) với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y = f( x) cắt trục tung tại điểm có tung độ là bao nhiêu?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai+ Ta có đạo hàm f’ (x) = 3ax2+ 2bx+c .
+ Dựa vào đồ thị hàm số y= f’( x) ta thấy đồ thị hàm số đi qua các điểm (0 ; 0) ; (1 ; -1) ; (2 ; 0) nên a = 1/3 ; b = -1 ; c = 0.
Do vậy hàm số cần tìm có dạng y= 1/3 x3 - x2+ d .
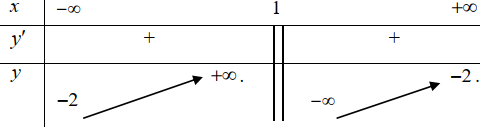
Điểm tiếp xúc với trục hoành là cực trị của đồ thị hàm số và tại đó ta có x = 0 hoặc x = 2.
+ Vì đồ thị hàm số y = f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương nên đồ thị hàm số tiếp xúc trục hoành tại điểm x = 2 nghĩa là:
f(2) = 0 hay 8/3 - 4+ d= 0 nên d = 4/3.
.jpg.png)
.png)
.png)