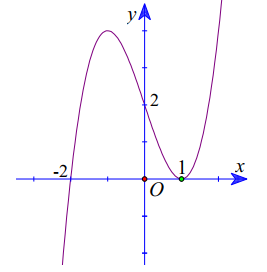
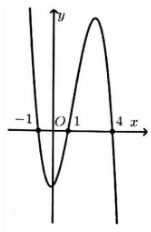
Cho hàm số y=f(x) có đạo hàm và liên tục trên tập số thực R. Biết đồ thị hàm số y=f′(x) như hình vẽ bên dưới. Hỏi đồ thị hàm số \(y=f(−2x+4)\) có bao nhiêu điểm cực tiểu?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDựa vào đồ thị ta có:
\(\begin{array}{l} y' = f'\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l} x > 4\\ - 1 < x < 1 \end{array} \right.\\ y' = f'\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l} x < - 1\\ 1 < x < 4 \end{array} \right. \end{array}\)
Xét hàm số \(y = f( - 2x + 4) \Rightarrow y' = - 2.f'( - 2x + 4)\).
Ta có:
\(\begin{array}{*{20}{l}} {y' = 0 \Leftrightarrow f'( - 2x + 4) = 0}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} \Leftrightarrow \left[ {\begin{array}{*{20}{l}} { - 2x + 4 = - 1}\\ { - 2x + 4 = 1}\\ { - 2x + 4 = 4} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = \frac{5}{2}}\\ {x = \frac{3}{2}}\\ {x = 0} \end{array}} \right.}\\ {y' < 0 \Leftrightarrow f'\left( { - 2x + 4} \right) > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} { - 2x + 4 < - 1}\\ {1 < - 2x + 4 < 4} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x > \frac{5}{2}}\\ {0 < x < \frac{3}{2}} \end{array}} \right. \Leftrightarrow x \in \left( {0;\frac{3}{2}} \right) \cup \left( {\frac{5}{2}; + \infty } \right)}\\ {y' > 0 \Leftrightarrow f'\left( { - 2x + 4} \right) < 0 \Leftrightarrow \left[ \begin{array}{l} - 1 < - 2x + 4 < 1\\ - 2x + 4 > 4 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} \frac{3}{2} < x < \frac{5}{2}\\ x < 0 \end{array} \right. \Leftrightarrow x \in \left( { - \infty ;0} \right) \cup \left( {\frac{3}{2};\frac{5}{2}} \right)} \end{array}\)
Ta có bảng xét dấu
Dựa vào bảng xét dấu hàm số có một điểm cực tiểu
Câu hỏi liên quan
-
Cho hàm số \(y = - {x^3} + 3{x^2} + 6x\). Hàm số đạt cực trị tại hai điểm x1, x2. Khi đó giá trị của biểu thức \(S = {x_1}^2 + {x_2}^{2\;}\) bằng:
-
Tính theo m khoảng cách giữa điểm cực đại và điểm cực tiểu ( nếu có) của đồ thị hàm số: \(y = \frac{1}{3}{x^3} - m{x^2} - x + m + 1\)
-
Điểm cực đại của hàm số \(y = \frac{1}{4}{x^4} - 2{x^2} + 5\) là:
-
Tìm các giá trị của tham số m để hàm số \(y = m{x^4} + \left( {{m^2} - 4m + 3} \right){x^2} + 2m - 1\) có ba điểm cực trị
-
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên.
.png)
Tọa độ điểm cực đại của đồ thị hàm số \(y = f\left( x \right)\) là
-
Hàm số y = (m – 3)x3 – 2mx2 + 3 không có cực trị khi
-
Hàm số y =f(x) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
-
Hàm số \(y = mx⁴ + (m -1) x² +1- 2m\)có một điểm cực trị khi
-
Điểm cực tiểu của đồ thị hàm số \(y = \frac{1}{4}{x^4} + 2{x^2} - 2\) là:
-
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=(m+1) x^{4}-m x^{2}+\frac{3}{2}\) chỉ có cực tiểu mà không có cực đại.
-
Hàm số \(y = \frac{{2x – 5}}{{x + 1}}\) có bao nhiêu điểm cực trị?
-
Tìm điểm cực đại xCĐ (nếu có) của hàm số \(y = \sqrt {x - 3} - \sqrt {6 - x} \)
-
Tìm giá trị cực đại yCĐ của hàm số y = −x4+2x2−5
-
Cho hàm số \(y = {x^7} - {x^5}\). Khẳng định nào sau đây là đúng
-
Tìm tất cả các điểm cực tiểu của hàm số y = 2 cos 2x + 3
-
Cho hàm số \(y = – {x^4} + 2017{x^2} – 2018\). Số điểm cực trị của đồ thị hàm số là
-
Cho hàm số \(y = {x^4} – \frac{2}{3}{x^3} – {x^2}.\) Mệnh đề nào sau đây là đúng?
-
Khẳng định nào sau đây là khẳng định sai về hàm số \(y = \frac{{2x - 1}}{{x + 1}}\)?
-
Cho hàm số y = f (x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:
Khẳng định nào sau đây đúng?
-
Cho hàm số f (x) có bảng biến thiên như sau:
.png)
hàm số đã cho đạt cực tiểu tại
