Cho hàm số y=f(x). Hàm số y =f'(x)có đồ thị như hình bên.

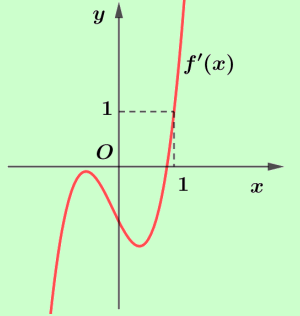
Hàm số \(g(x)=f\left(x^{2}+2 x\right)-x^{2}-2 x\) đồng biến trên khoảng nào dưới đây?

A. \((-1-\sqrt{2} ;-1)\)

B. \((-1-\sqrt{2} ;-1+\sqrt{2})\)

C. \((-1 ;-1+\sqrt{2})\)

D. \((-1 ;+\infty)\)

Suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Môn: Toán Lớp 12

Chủ đề: Ứng Dụng Đạo Hàm Để Khảo Sát Và Vẽ Đồ Thị Của Hàm Số

Bài: Sự đồng biến, nghịch biến của hàm số

Lời giải:

Báo sai

\(\begin{array}{l} \text { Ta có: } g(x)=f\left(x^{2}+2 x\right)-x^{2}-2 x \\ \Rightarrow g^{\prime}(x)=(2 x+2) f^{\prime}\left(x^{2}+2 x\right)-2 x-2=2(x+1)\left[f^{\prime}\left(x^{2}+2 x\right)-1\right] \\ \Rightarrow g^{\prime}(x)=0 \Leftrightarrow 2(x+1)\left[f^{\prime}\left(x^{2}+2 x\right)-1\right]=0 \Leftrightarrow x=-1, x=-1+\sqrt{2}, x=-1-\sqrt{2} \end{array}\)

Xét \(g^{\prime}(x)>0 \Leftrightarrow\left[\begin{array}{ll} \left\{\begin{array}{l} x+1>0 \\ f^{\prime}\left(x^{2}+2 x\right)>1 \end{array}\right.\,\,\,(I) \\ \left\{\begin{array}{l} x+1<0 \\ f^{\prime}\left(x^{2}+2 x\right)<1 \end{array}\right.\,\,\,(II) \end{array}\right.\)

Xét sự tương giao của đồ thị hàm số \(y=f^{\prime}(x) \text { và } y=1\).

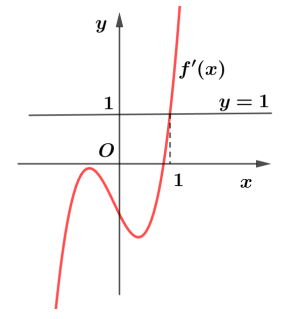
Dựa vào đồ thị ta có: \(f^{\prime}\left(x^{2}+2 x\right)>1 \Leftrightarrow x^{2}+2 x>1 \text { và } f^{\prime}\left(x^{2}+2 x\right)<1 \Leftrightarrow x^{2}+2 x<1\)

Xét hệ (I): \(\left\{\begin{array}{l} x+1>0 \\ f^{\prime}\left(x^{2}+2 x\right)>1 \end{array} \Leftrightarrow\left\{\begin{array}{l} x>-1 \\ x^{2}+2 x>1 \end{array}\right.\right.\)

\(\Leftrightarrow \left\{ \begin{array}{l} x > - 1\\ \left[ {\begin{array}{*{20}{l}} {x > - 1 + \sqrt 2 }\\ {x < - 1 - \sqrt 2 } \end{array}} \right. \end{array} \right. \Leftrightarrow x > - 1 + \sqrt 2 \)

Xét hệ (II): \(\left\{\begin{array}{l} x+1<0 \\ f^{\prime}\left(x^{2}+2 x\right)<1 \end{array} \Leftrightarrow\left\{\begin{array}{l} x<-1 \\ x^{2}+2 x<1 \end{array} \Leftrightarrow\left\{\begin{array}{l} x<-1 \\ -1-\sqrt{2}<x<-1+\sqrt{2} \end{array}\right.\right.\right.\)

\(\Leftrightarrow-1-\sqrt{2}<x<-1\)

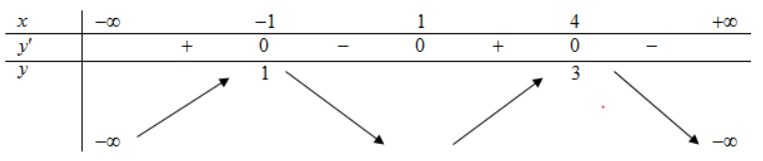
Vậy hàm số g (x) đồng biến trên khoảng \((-1-\sqrt{2} ;-1) \text { và }(-1+\sqrt{2} ;+\infty)\)