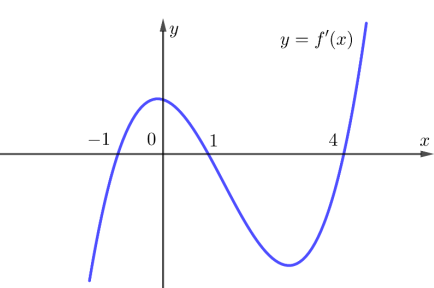
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) có f (0)=0 và đồ thị hàm số y=f'(x)như hình vẽ dưới đây
Hàm số \(y=\left|3 f(x)-x^{3}\right|\)3 đồng biến trên khoảng:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiXét hàm số \(g(x)=3 f(x)-x^{3} \text { có } g^{\prime}(x)=3 f^{\prime}(x)-3 x^{2}=0 \Leftrightarrow f^{\prime}(x)=x^{2}\)
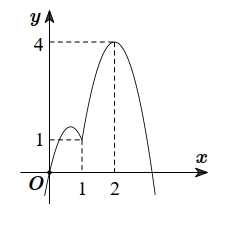
Vẽ đồ thị hàm số \(y=x^{2}\) cắt đồ thị y=f'(x) tại 3 điểm \(x=0, x=1, x=2\) (như hình vẽ).
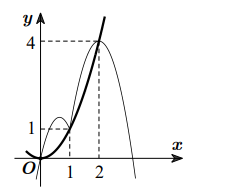
Từ đây ta có bảng biến thiên của hàm số\(y=g(x)\) (như hình trên).
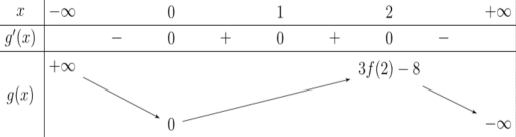
Dùng phép đối xứng đồ thị, ta thu được hàm số \(y=|g(x)|\) đồng biến trên khoảng \((0 ; 2)\,\, và \,\,(a ;+\infty)\,\, với \,\,a \geq 2\)
ADMICRO
YOMEDIA
ZUNIA9
.png)