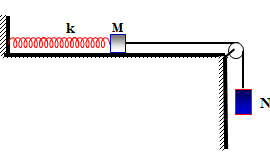
Cho hệ vật gồm lò xo nhẹ có độ cứng k = 20 N/m, vật M có khối lượng 30 g được nối với vật N có khối lượng 150 g bằng một sợi dây không dãn vắt qua ròng rọc như hình bên. Bỏ qua mọi ma sát, bỏ qua khối lượng dây và ròng rọc. Ban đầu giữ M tại vị trí để lò xo không biến dạng, N ở xa mặt đất. Thả nhẹ M để cả hai vật cùng chuyển động, sau 0,2 s thì dây bị đứt. Sau khi dây đứt, M dao động điều hòa trên mặt phẳng nằm ngang với biên độ A. Lấy g = 10m/s2, \(\pi ^2 \approx 10\) .Giá trị của A bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiLúc đầu hệ hai vật dao động quanh vị trí cân bằng của chúng với biên độ
\( {A_{12}} = {\rm{\Delta }}l\) với \( {\rm{\Delta }}l = \frac{{{m_N}g}}{k} = \frac{{0,15.10}}{{20}} = 0,075 = 7,5cm\)
Chu kỳ hệ 2 vật: \( {T_{12}} = 2\sqrt {\frac{{{\pi ^2}\left( {{m_M} + {m_N}} \right)}}{k}} = 0,6s\)
Sau 0,2 s kể từ khi hệ dao động \( t = 0,2s = \frac{{{T_{12}}}}{3} = \frac{{{T_{12}}}}{4} + \frac{{{T_{12}}}}{{12}}\)
Cả hai vật đi được quãng đường: \( {A_{12}} + \frac{{{A_{12}}}}{2}\)
Lúc đó cà hai vật cùng vận tốc
\( \left| {{v_{12}}} \right| = \frac{{\sqrt 3 }}{2}{v_{max}} = \frac{{25\sqrt {30} }}{2}cm/s\)
Lúc sau vật 2 tách khỏi hệ chỉ còn vật 1 tham gia dao động.
Vật 1 sẽ dao động quanh vị trí cân bằng của nó chính là vị trí lò xo không biến dạng với tần số góc mới \(\omega = \sqrt {\frac{k}{{{m_M}}}} = \frac{{20\sqrt {15} }}{3}\left( {rad/s} \right)\)
Như vậy so với vị trí cân bằng của vật 1, vật 1 có tọa độ vận tốc: \(\left\{ \begin{array}{l} x = 7,5 + \frac{{7,5}}{2} = 11,25cm\\ |v| = \frac{{25\sqrt {30} }}{2}cm/s \end{array} \right.\)
Biên độ dao động mới
\( A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = 11,558cm\)
Đáp án cần chọn là: A