Cho hình hộp chữ nhật \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có \(A B=A A^{\prime}=a\), đường chéo A'C tạo với mặt đáy (ABCD) một góc \(\alpha\) thỏa \(\cot \alpha=\sqrt{5}\) Thể tích khối hộp đã cho bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai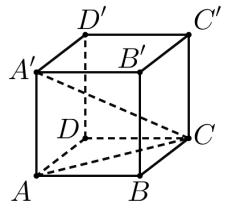
Xác định:\(\alpha=\left(\widehat{A^{\prime} C,(A B C D)}\right)=\left(\widehat{A^{\prime} C, A C}\right)=\widehat{A^{\prime} C A}\)
Ta có \(\left\{\begin{array}{l} A C=A A^{\prime} \cdot \cot \alpha=a \sqrt{5} \\ A B=A A^{\prime}=a \end{array} \Rightarrow B C=\sqrt{A C^{2}-A B^{2}}=2 a\right.\)
Vậy \(V_{A B C D . A^{\prime} B^{\prime} C^{\prime} D^{\prime}}=A A^{\prime} \cdot A B \cdot B C=2 a^{3}\)
Câu hỏi liên quan
-
Cho khối chóp \(S.ABCD\) có đáy là hình vuông cạnh a, \(SA\) vuông góc với đáy và \(SC\) tạo với mặt phẳng \(\left( SAB \right)\) một góc \({{30}^{0}}.\) Tính thể tích \(V\) của khối chóp đã cho.
-
Cho hình lập phương ABCD.A’B’C’D’. Tính thể tích V của hình lập phương biết rằng khoảng cách từ trung điểm I của AB đến mặt phẳng A’B’CD bằng \(\frac{a}{\sqrt{2}}\)
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Biết \(SA \bot \left( {ABC} \right)\) và \(SA = a\sqrt 3 \). Tính thể tích khối chóp S.ABC.
-
Cho hình lập phương ABCD.A’B’CD’ cạnh a. Trên cạnh AA’ kéo dài về phía A’ lấy điểm M trên cạnh BC kéo dài về phía C lấy điểm N sao cho MN cắt cạnh C’D’ . Tính giá trị nhỏ nhất của MN?
-
Tính thể tích V của khối lập phương \(ABCD.{A_1}{B_1}C{}_1{D_1}\), biết diện tích mặt chéo \(AC{C_1}{A_1}\) bằng \(4\sqrt 2 {a^2}\)
-
Cho hình chóp \(S.ABCD,\) đáy \(ABCD\) là hình thang vuông tại \(A,D;AB=AD=2a,CD=a.\) Góc giữa hai mặt phẳng \(\left( SBC \right)\) và \(\left( ABCD \right)\) bằng \({{60}^{0}}.\) Gọi \(I\) là trung điểm của \(AD,\) biết hai mặt phẳng \(\left( SBI \right),\left( SCI \right)\) cùng vuông góc với mặt phẳng \(\left( ABCD \right).\) Tính thể tích khối chóp \(S.ABCD.\)
-
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh 2a. Cạnh bên SA vuông góc với đáy và \(SA = a\sqrt 3 \). Tính thể tíchV của khối chóp S.ABC.
-
Cho khối tự diện OABC có OA, OB, OC đôi một vuông góc và OA = a; OB = b; OC = c. Thể tích khối tứ diện OABC được tính theo công thức nào sau đây
-
Thể tích của khối có 5 mặt hình chữ nhật, 4 mặt tam giác với kích thước được cho như hình vẽ là
.png)
-
Cho khối hộp \(ABCD.A'B'C'D'\) có độ dài cạnh bên bằng a; đáy là hình thoi, diện tích của hai mặt chéo là \({{S}_{1}}\) và \({{S}_{2}}\); góc giữa hai mặt phẳng chứa hai mặt chéo là \(\alpha .\) Tính thể tích V của khối hộp đã cho.
-
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt đáy, góc giữa SC và mặt đáy bằng 300. Thể tích khối chóp S.ABC là:
-
Câu 1.Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy \(\left( ABCD \right)\). Biết \(SD=2a\sqrt{3}\) và góc tạo bởi đường thẳng SC và mặt phẳng \(\left( ABCD \right)\) bằng \({{30}^{0}}\). Tính thể tích \(V\) của khối chóp S.ABCD.
-
Cho hình lập phương có thể tích bằng 27. Diện tích toàn phần của hình lập phương là:
-
Cho hình chóp \(S.ABCD\) có đáy ABCD là hình chữ nhật, mặt bên \(SAD\) là tam giác vuông tại \(S\). Hình chiếu vuông góc của \(S\) trên mặt phẳng đáy là điểm H thuộc cạnh AD sao cho HA=3HD. Biết rằng \(SA=2a\sqrt{3}\) và \(SC\) tạo với đáy một góc bằng \(30{}^\circ \). Tính theo a thể tích \(V\) của khối chóp \(S.ABCD\).
-
Cho khối chóp S.ABC. Trên các đoạn SA, SB, SC lần lượt lấy ba điểm A', B', C’ sao cho \(SA'=\frac{1}{2}SA;SB'=\frac{1}{3}SB;SC'=\frac{1}{4}SC\). Khi đó tỉ số thể tích của hai khối chóp S.A'B'C' và S.ABC bằng:
-
Cho hình lập phương \(ABCD.ABCD\). Mặt phẳng (BDC’) chia khối lập phương thành 2 phần có tỉ lệ thể tích phần nhỏ so với phần lớn là :
-
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(B\), \(AB=a\), \(AC=2a\). Hình chiếu vuông góc của \(S\) lên \(\left( ABC \right)\) là trung điểm \(M\) của \(AC\). Góc giữa \(SB\) và đáy bằng \(60{}^\circ \). Thể tích \(S.ABC\) là bao nhiêu?
-
Cho hình lăng trụ có tất cả các cạnh đều bằng \(a\), đáy là lục giác đều, góc tạo bởi cạnh bên và mặt đáy là\(60{}^\circ \). Tính thể tích khối lăng trụ
-
Cho hình chóp S. ABCD có đáy là hình thoi cạnh a, tam giác ABC đều. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD tạo với mặt phẳng đáy góc 300 Thể tích của khối chóp đã cho bằng
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SO tạo với mặt phẳng đáy một góc 450. Tính thể tích V của khối chóp S.ABCD.
