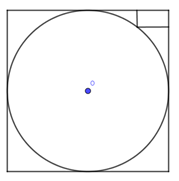
Cho hình trụ (T) có ( C ), (C') ) là hai đường tròn đáy nội tiếp hai mặt đối diện của một hình lập phương. Biết rằng, trong tam giác cong tạo bởi đường tròn (C) và hình vuông ngoại tiếp của (C) có một hình chữ nhật kích thước 1 x 2 (như hình vẽ dưới đây). Thể tích của khối trụ (T) là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
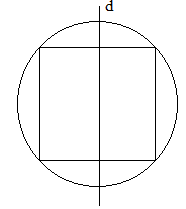
Báo saiGắn hệ trục tọa độ trong mặt phẳng chứa đường tròn (C) như hình vẽ.
Phương trình đường tròn (C): \( {\left( {x - R} \right)^2} + {\left( {y - R} \right)^2} = {R^2},{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (R > 2)\)
Điểm (1;2) thuộc (C)
\(\begin{array}{l} \Rightarrow {(1 - R)^2} + {(2 - R)^2} = {R^2} \Leftrightarrow {R^2} - 6R + 5 = 0\\ \to \left[ \begin{array}{l} R = 1\\ R = 5 \end{array} \right. \to R = 5 \end{array}\)
⇒ Chiều cao của khối trụ h=2R=10
Thể tích khối trụ là: \( V = \pi {R^2}h = \pi {.5^2}.10 = 250\pi \)