Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt 3 \), cạnh SA vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và SB tạo với đáy một góc \(60^\circ \). Tính thể tích V của khối chóp S.ABCD.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai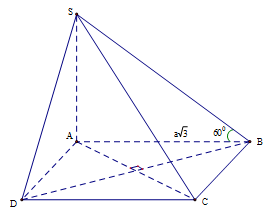
\(SA \bot \left( {ABCD} \right) \Rightarrow AB\) là hình chiếu vuông góc của SB lên mặt phẳng \(\left( {ABCD} \right)\)
\( \Rightarrow \widehat {\left( {SB,\left( {ABCD} \right)} \right)} = \widehat {\left( {SB,AB} \right)} = \widehat {SBA} = 60^\circ \)
Trong tam giác vuông SAB,
\(SA = \tan 60^\circ .AB = \sqrt 3 .a\sqrt 3 = 3a\)
\({S_{ABCD}} = A{B^2} = {\left( {a\sqrt 3 } \right)^2} = 3{a^2}\)
Vậy thể tích V của khối chóp S.ABCD là
\(V = \frac{1}{3}.{S_{ABCD}}.SA = \frac{1}{3}.3{a^2}.3a = 3{a^{.3}}\)











