Cho lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy là tam giác cân tại A, AB=AC=2a, \(\widehat{CAB}={{120}^{{}^\circ }}\), góc giữa \(\left( {A}'BC \right)\) và \(\left( ABC \right)\) là \(45{}^\circ \). Tính thể tích lăng trụ đã cho.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai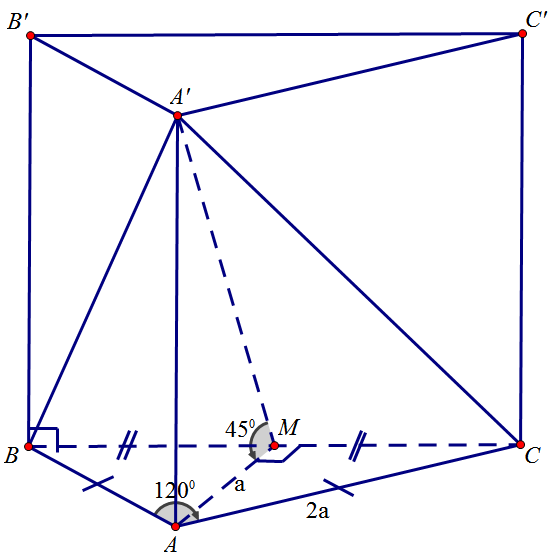
Gọi M là trung điểm của \(BC\). Ta có \(AM\bot BC\) và \(\widehat{CAM}=60{}^\circ \)( do\(\Delta ABC\) cân tại A)
Ta xác định được góc giữa \(\left( {A}'BC \right)\) và \(\left( ABC \right)\) là \(\widehat{{A}'MA}=45{}^\circ \)
Ta có \({{S}_{\Delta ABC}}=\frac{1}{2}AB.AC.\text{sin}\widehat{BAC} =\frac{1}{2}.{{\left( 2a \right)}^{2}}\sin 120{}^\circ ={{a}^{2}}\sqrt{3}\) và
\(AM=AC\cos \widehat{MAC} =2a.\text{cos}60{}^\circ =a; A{A}'=AM.\tan \widehat{{A}'MA}=a\)
Vậy\({{V}_{ABC.{A}'{B}'{C}'}}=A{A}'.{{S}_{\Delta ABC}}={{a}^{3}}\sqrt{3}\) (đơn vị thể tích).