Cho mạch điện như hình vẽ. Cho biết hiệu điện thế U = 24V.
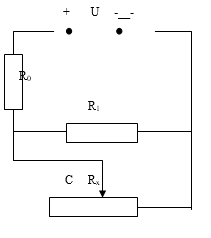
Các điện trở R0 = 6 Ω, R1 = 18 Ω, Rx là một biến trở, dây nối có điện trở không đáng kể. Với giá trị nào của Rx thì công suất tiêu thụ trên Rx đạt cực đại? Tính công suất cực đại này.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiCông suất tiêu thụ trên Rx:
\(\begin{array}{l} {P_x}\; = {\rm{ }}{I^2}.{R_x} = {\left( {\frac{{18}}{{4,5 + {R_x}}}} \right)^2}\\ {R_x} = \frac{{324}}{{{R_x} + \frac{{20,25}}{{{R_x}}} + 9}} \end{array}\)
Để PX cực đại thì mẫu số phải cực tiểu, nhưng tích của 2 số không âm:
\({R_x}.\frac{{20,25}}{{{R_x}}} = 20,25\)
→ tổng của chúng sẽ cực tiểu khi:
\({R_x} = \frac{{20,25}}{{{R_x}}} \Rightarrow {R_x} = 4,5\Omega \)
Lúc đó giá trị cực đại của công suất: \({P_{x(m{\rm{ax)}}}}\; = {\rm{ }}\frac{{324}}{{4,5 + 4,5 + 9}} = 18W\)
.png)
.png)
.png)
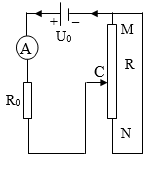
.png)












