Cho một ngũ giác đều và một phép dời hình f . Biết rằng \(\mathrm{f}(\mathrm{A})=\mathrm{C}, \mathrm{f}(\mathrm{E})=\mathrm{B} \text { và } \mathrm{f}(\mathrm{D})=\mathrm{A}\) . Ảnh của điểm C là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai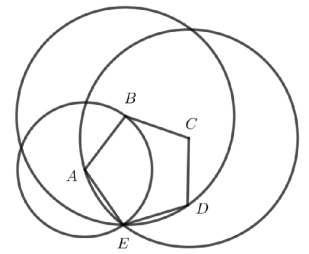
Nếu \(\mathrm{M}=\mathrm{f}(\mathrm{C}) \text { ta có } \mathrm{CA}=\mathrm{CM}(\text { do } \mathrm{f}(\mathrm{A})=\mathrm{C})(1)\)
\(\begin{array}{l} \mathrm{CE}=\mathrm{MB}(\mathrm{do\,\,f}(\mathrm{E})=\mathrm{B})(2) \\ \mathrm{CD}=\mathrm{MA}(\operatorname{do\,\,f}(\mathrm{D})=\mathrm{A})(3) \end{array}\)
\((1) \Leftrightarrow\)M thuộc đường tròn tâm C bán kính CA
\((2) \Leftrightarrow\) M thuộc đường tròn tâm B bán kính CE=BE
\((3) \Leftrightarrow\) M thuộc đường tròn tâm A bán kính CD=AE .
Vậy \(\mathrm{M} \equiv \mathrm{E}\)











