Cho phương trình \(x^{3}-3 x^{2}+1-m=0(1)\) Điều kiện của tham số m để (1)có ba nghiệm phân biệt thỏa\(x_{1}<1<x_{2}<x_{3}\) khi
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(x^{3}-3 x^{2}+1-m=0\) là phương trình hoành độ giao điểm giữa hai đồ thị hàm số \(y=x^{3}-3 x^{2}+1 \text { và } y=m\) (là đường thẳng song song hoặc trùng với Ox ).
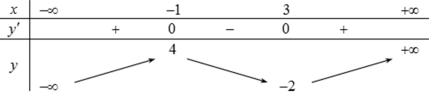
Xét \(y=x^{3}-3 x^{2}+1\) . Tập xác định: \(D=\mathbb{R}\).
\(\begin{array}{l} y^{\prime}=3 x^{2}-6 x \\ y^{\prime}=0 \Leftrightarrow 3 x^{2}-6 x=0 \Leftrightarrow\left[\begin{array}{l} x=0 \Rightarrow y=1 \\ x=2 \Rightarrow y=-3 \end{array}\right. \end{array}\)
\(x=1 \Rightarrow y=-1\)
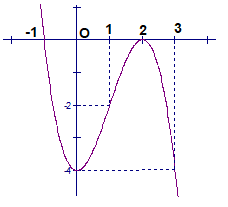
Đồ thị hàm số
Dựa vào đồ thị, số nghiệm của phương trình (1) chính là số giao điểm của đồ thị \(y=x^{3}-3 x^{2}+1\)và đường thẳng y=m .
Do đó, yêu cầu bài toán \(\Leftrightarrow-3<m<-1\)
Câu hỏi liên quan
-
Gọi M, N là giao điểm của y = x+1 và \(y\; = \frac{{\;2x + 4\;}}{{x - 1}}\) Khi đó hoành độ trung điểm của I của đoạn thẳng MN bằng
-
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với a > 0 có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
-
Giá trị của m để phương trình \(x+\sqrt{2 x^{2}+1}=m\) có nghiệm là:
-
Tìm trên mỗi nhánh của đồ thị (C): \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbb % a9q8WqFfeaY-biLkVcLq-JHqpepeea0-as0Fb9pgeaYRXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacqGH9a % qpdaWcaaqaaiaaisdacaWG4bGaeyOeI0IaaGyoaaqaaiaadIhacqGH % sislcaaIZaaaaaaa!3E0F! y = \frac{{4x - 9}}{{x - 3}}\) các điểm \(M_1;M_2\) để độ dài \(M_1M_2\) đạt giá trị nhỏ nhất, giá trị nhỏ nhất đó bằng:
-
Cho hàm số \(y=f(x)=x^3+3x^2–x–3\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(y=||x|^3+3x^2–|x|–3|\) có dạng nào trong các đáp án sau đây?
-
Biết \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaabm % aabaGaamiEamaaBaaaleaacaWGbbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGbbaabeaaaOGaayjkaiaawMcaaaaa!3E80! A\left( {{x_A};\,{y_A}} \right)\),\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaWGcbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGcbaabeaaaOGaayjkaiaawMcaaaaa!3E83! B\left( {{x_B};\,{y_B}} \right)\) là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaWGcbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGcbaabeaaaOGaayjkaiaawMcaaaaa!3E83! B\left( {{x_B};\,{y_B}} \right)\) sao cho đoạn thẳng AB có độ dài nhỏ nhất. Tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiabg2 % da9iaadIhadaqhaaWcbaGaamyqaaqaaiaaikdaaaGccqGHRaWkcaWG % 4bWaa0baaSqaaiaadkeaaeaacaaIYaaaaOGaey4kaSIaamyEamaaBa % aaleaacaWGbbaabeaakiaac6cacaWG5bWaaSbaaSqaaiaadkeaaeqa % aaaa!439D! P = x_A^2 + x_B^2 + {y_A}.{y_B}\).
-
Viết phương trình tiếp tuyến d của đồ thị (C) : \(y = \frac{{2x + 1}}{{x + 1}}\) biết d cách đều điểm A( 2; 4) và B( -4; -2).
-
Tất cả giá trị của tham số m để phương trình \(x^{4}-2 x^{2}-m+3=0\) có bốn nghiệm phân biệt là
-
Đường cong hình bên dưới là đồ thị hàm số nào trong 4 hàm số sau:
-
Bảng biến thiên trong hình vẽ dưới đây là bảng biến thiên của hàm số nào?
-
Trong không gian với hệ tọa độ Oxyz, viết phương trình tham số của đường thẳng nằm trong mặt phẳng y + 2z = 0 và cắt hai đường thẳng d1: \(\left\{ \begin{array}{l} x = 1 - t\\ y = t\\ z = 4t \end{array} \right.;{d_2}:\left\{ \begin{array}{l} x = 2 - t\prime \\ y = 4 + 2t\prime \\ z = 1 \end{array} \right.\)
-
Hoành độ giao điểm của đồ thị (C): \(y = \frac{{2x + 1}}{{2x – 1}}\) và đường thẳng d:y = x + 2.
-
Đồ thị hàm số \(y = {\log _2}\left( {{x^2} + 2} \right)\) cắt trục tung tại điểm có tung độ bằng
-
Tất cả giá trị của tham số m để đồ thị hàm số \(\left( C \right):y = – 2{x^3} + 3{x^2} + 2m – 1\) cắt trục hoành tại ba điểm phân biệt là
-
Trong các mệnh đề sau, mệnh đề nào đúng?
A. I(1; 0) là tâm đối xứng của y=x+1x−1y=x+1x-1
B. I(1; 0) là tâm đối xứng của y=−x3+3x2−2y=-x3+3x2-2
C. I(1; 0) là điểm thuộc đồ thị y=x+1x−1y=x+1x-1
D. I(1; 0) là giao điểm của y=x3−3x2−2y=x3-3x2-2 với trục hoành.
-
Giao điểm giữa đồ thị \((C):y = \frac{{{x^2} – 2x – 3}}{{x – 1}}\) và đường thẳng \(\left( d \right):y = x + 1\) là
-
Tìm m để bất phương trình \({x^4} + 2{x^2} \ge m\) luôn đúng.
-
Cho hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\). Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng y = 3x −1
-
Cho hàm số \(y = \frac{{x + 2}}{{2x + 3}}\left( 1 \right)\). Viết phương trình tiếp tuyến của đồ thị hàm số đã cho, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB cân tại gốc tọa độ.
-
Cho hàm số \(y = \frac{1}{3}{x^3} + {x^2} - 2\)
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình y'' = 0 là
