Cho tứ diện đều ABCD có cạnh bằng a,điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó diện tích thiết diện của hình tứ diện cắt bởi mp qua M và song song với mp(ACD) là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai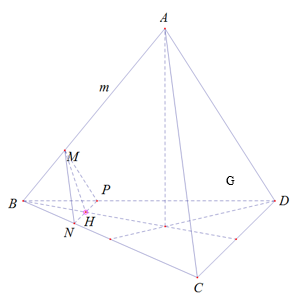
Trong (ABC) kẻ MN // AC ( N ∈ BC)
Trong (ABD) kẻ MP // AD ( P ∈ BD)
⇒ (MNP) là mặt phẳng cần tìm
Xét tam giác MNP có MN = MP = NP (= a−m)
⇒ tam giác MNP đều
Mà NP // CD và BG là trung tuyến tam giác BCD
⇒ BG cắt NP tại H là trung điểm NP
⇒ MH là đường cao tam giác MNP
Ta có: PH = \(\frac{{a - m}}{2}\) và MP = a – m. Áp dụng định lý pitago, ta có: MH = \(\frac{{\sqrt 3 }}{2}\left( {a - m} \right)\)
Và NP = a – m
SMNP = \(\frac{{MH.NP}}{2} = \frac{{\sqrt 3 }}{4}{\left( {a - m} \right)^2}\)
Câu hỏi liên quan
-
Cho hình chóp S. ABCD, đáy là hình bình hành ABCD, điểm N thuộc cạnh SC sao cho 2NC = NS, M là trọng tâm của tam giác CBD. Phát biểu nào sau đây là đúng?
-
Cho hình chóp S.ABCD, O là giao điểm của AC và BD, phát biểu nào sau đây là đúng?
-
Chọn khẳng định sai trong các khẳng định sau?
-
Trong các khẳng định sau, khẳng định nào đúng?
-
Cho hình tứ diện ABCD và ba điểm P, Q, R lần lượt lấy trên ba cạnh AB, CD, BC. Cho PR // AC và CQ = QD. Gọi giao điểm của AD và (PQR) là S. Chọn khẳng định đúng
-
Cho hình chóp S ABCD . . Điểm C' nằm trên cạnh SC . Thiết diện của hình chóp với mp ( ABC') là một đa giác có bao nhiêu cạnh?
-
Có một và chỉ một mặt phẳng đi qua
-
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Gọi P là giao điểm của SC và (AND). AN cắt DP tại I. SABI là hình gì?
-
Cho bốn điểm A,B,C,D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại I . Điểm I không thuộc mặt phẳng nào sao đây:
-
Ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt. khẳng định nào sau đây là đúng?
-
Hình nào sau đây vẽ đúng quy tắc?
-
Trong các mệnh đề sau, mệnh đề nào Đúng?
-
Nếu hai mặt phẳng phân biệt có điểm chung thì tất cả những điểm chung của chúng sẽ nằm trên:
-
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và A’B’C’. Thiết diện tạo bởi mặt phẳng (AIJ) với hình lăng trụ đã cho là:
-
Trong các hình sau: Các hình có thể là hình biểu diễn của một hình tứ diện là:
-
Cho hình chóp S.ABCD . Gọi I là trung điểm của SD , J là điểm trên SC và không trùng trung điểm SC . Giao tuyến của hai mặt phẳng (ABCD) và (AIJ) là:
-
Cho hình hộp ABCD.EFHG, khẳng định nào sau đây là sai?
-
Cho hình chóp S.ABCDE, phát biều nào sau đây là đúng?
-
Cho hình chóp S.ABCD có đáy là hình thang ABCD (AB//CD) . Khẳng định nào sau đây sai?
-
Cho 4 điểm không đồng phẳng A, B, C, D. Khi đó giao tuyến của mp (ABC) và mp (BCD) là:
