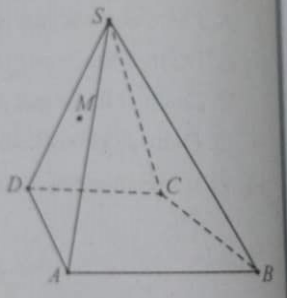
Cho tứ diện đều SABC. Gọi I là trung điểm của AB, M là một điểm di động trên đoạn AI. Gọi (P) là mp qua M và song song với mp(SIC); biết AM = x. Thiết diện tạo bởi mp(P) và tứ diện SABC có chu vi là:

Câu hỏi liên quan

• Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm SA. Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (IBC) là:

• Cho tứ diện đều ABCD cạnh a. I, J lần lượt là trung điểm của AC và BC. Gọi K là giao điểm trên cạnh BD với KB = 2KD. Thiết diện của tứ diện với mặt phẳng (IJK) là hình gì?

• Cho hình chóp S.ABCD . Gọi I là trung điểm của SD , J là điểm trên SC và không trùng trung điểm SC . Giao tuyến của hai mặt phẳng (ABCD) và (AIJ) là:

ZUNIA12

• Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và điểm M ở trên cạnh SB . Mặt phẳng (ADM) cắt hình chóp theo thiết diện là

• Trong mp \((\alpha)\), cho bốn điểm A,B,C,D trong đó không có ba điểm nào thẳng hàng. Điểm (S notin mp \((\alpha)\) ). Có mấy mặt phẳng tạo bởi S và hai trong số bốn điểm nói trên?

• Trong các mệnh đề sau, mệnh đề nào đúng?

• Cho tứ giác lồi ABCD và điểm S không thuộc mp (ABCD). Có bao nhiêu mặt phẳng phân biệt xác định bởi 3 trong số các điểm A,B,C,D,S?

• Trong các khẳng định sau, khẳng định nào đúng?

• Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là :

• Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I,J lần lượt là trung điểm của AB và BC. Khi đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với:

• Giả sử (P) , (Q), (R) là ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt a, b, c trong đó a = (P) ∩ (R), b = (Q) ∩ (R), c = (P) ∩ (Q). Trong các mệnh đề sau, mệnh đề nào sai?

• Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:

• Cho bốn điểm A,B,C,D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại I . Điểm I không thuộc mặt phẳng nào sao đây:

• Trong không gian cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?

• Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CB. M là điểm thuộc cạnh SD. Khẳng định nào sau đây là đúng?

• Cho hình chóp S.ABCD. trên các cạnh AC, SC lấy lần lượt các điểm I, K sao cho: \(\frac{{SC}}{{SK}} = \frac{{AC}}{{AI}}\)

  mặt phẳng (α) đi qua IK cắt các đường thẳng AB, AD, SD, SB tại các điểm theo thứ tự là M, N, P, Q. Khẳng định nào sau đây là đúng?

• Trong các mệnh đề sau mệnh đề nào sai?

• Cho hình chóp A.BCD. gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AC, BD, AB, cD, AD, BC. Các điểm nào sau đây cùng thuộc một mặt phẳng?

• Cho hình chóp S.ABCDE, phát biều nào sau đây là đúng?

  

• Cho hình chóp S.ABCD, M là điểm nằm trong tam giác SAD. Phát biểu nào sau đây là đúng?