Có bao nhiêu giá trị nguyên ucra tham số m để hàm số \(y = x⁸ + (m - 2) x⁵ - (m² - 4) x⁴ + 1\) đạt cực tiểu tại x=0
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:
\(y = x⁸ + (m - 2) x⁵ - (m² - 4) x⁴ + 1 \Rightarrow y' = 8x⁷ + 5 (m - 2) x⁴ - 4 (m² - 4) x³ \\ y' = 0\Rightarrow x³ (8x⁴ + 5(m - 2) x - 4 (m² - 4)) = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l} x = 0\\ g\left( x \right) = 8{x^4} + 5\left( {m - 2} \right)x - 4\left( {{m^2} - 4} \right) = 0 \end{array} \right.\)
Xét hàm số : \(g ( x ) = 8x⁴ + 5(m - 2) x - 4 (m² - 4) \,\,\rm{có}\,\,g'( x) = 32x³ + 5(m - 2) . \)
Ta thấy g'(c)=0 có một nghiệm nên g(x)=0 có tối đa hai nghiệm.
+TH1: Nếu g(c)=0 có nghiệm \(x=0\Leftrightarrow x=-2\,\,\,\rm{hoặc}\,\,\, x=2\)
Với m=2 thì x=0 là nghiệm bội 4 của g(x). Khi đó x=0 là nghiệm bội 7 của y' và y' đổi dấu từ âm sang dương khi đi qua x=0 nên x=0 là một điểm cực tiểu của hàm số. Vậy m=2 thỏa mãn điều kiện bài toán.
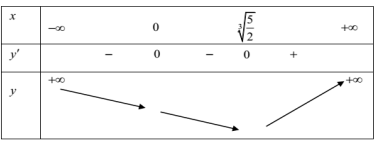
Với \(m = - 2 \Rightarrow g\left( x \right) = 8{x^4} - 20x = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = \sqrt[3]{{\frac{5}{2}}} \end{array} \right.\)
Khi đó x=0 là nghiệm đơn của g(x), hay x=0 là nghiệm bội 4 của y'. Vậy y' khi đi qua x=0 thì không đổi dấu. Nói cách khác x=0 không phải là cực trị của hàm số. Vậy m=-2 không thỏa mãn yêu cầu. Có thể thấy từ bảng biến thiên sau:
+ \(g(0)\ne0\Leftrightarrow m\ne\pm2\). Để hàm số đặt cực tiểu tại
\(x=0\Leftrightarrow g(0)>0\Leftrightarrow m^2-4>0\\ \Leftrightarrow -2<m<2\).
Do m là số nguyên nên \(m\in{\{-1;0;1\}}\).
Từ hai trường hợp suy ra có 4 giá trị nguyên của m thỏa mãn yêu cầu bài toán
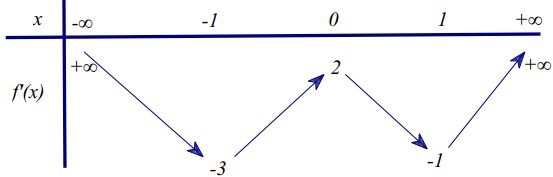
.jpg.png)











