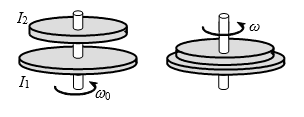
Hai đĩa tròn có cùng momen quán tính đối với trục quay đi qua tâm của các đĩa (hình bên). Lúc đầu, đĩa 2 (ở phía trên) đang đứng yên, đĩa 1 quay với tốc độ góc ω₀. Ma sát ở trục quay nhỏ không đáng kể. Sau đó, cho hai đĩa dính vào nhau, hệ quay với tốc độ góc ω. Động năng của hệ hai đĩa lúc sau so với lúc đầu

Một bánh đà đang quay đều với tốc độ 3 000 vòng/phút. Tác dụng một momen hãm không đổi 100 N.m vào bánh đà thì nó quay chậm dần đều và dừng lại sau 5 s. Tính momen quán tính của bánh đà đối với trục quay.

Xét một vật rắn đang ở trạng thái cân bằng. Đưa vật dời khỏi vị trí cân bằng một đoạn nhỏ rồi buông ra, nếu

Quả cầu đặc đồng chất có khối lượng m và bán kính R. Momen quán tính quả cầu đối với trục quay đi qua tâm quả cầu là

Một lò xo có độ cứng k đươc treo vào điểm cố định, đầu dưới treo vật có khối lượng m, tại nơi có gia tốc trọng trường g. Khi vật nằm cân bằng, độ biến dạng của lò xo là

Một bản mỏng kim loại đồng chất hình chữ T như trên hình III.2, với AB = CD = 60 cm ; EF= HG = 20 cm ; AD = BC =20 cm ; EH = FG =100 cm. Vị trí trọng tâm của bản cách đáy GH một đoạn

Một thanh chắn đường dài AB có chiều dài 7,8 m; trọng lượng 420 N và có trọng tâm cách đầu A của thanh 1,2 m. Thanh có thể quay quanh một trục O nằm ngang ở cách đầu A một khoảng 1,5 m như hình vẽ. Để giữ thanh nằm ngang ta phải tác dụng lên đầu B của thanh một lực có độ lớn bao nhiêu  

Mô men lực tác dụng lên một vật là đại lượng:

Nhận xét nào dưới đây về hợp lực của hai lực song song và cùng chiều là không đúng?

Tác dụng một lực F có giá đi qua trọng tâm của một vật thì vật đó sẽ

Một người khiêng một vật vật nặng 1000N bằng một đòn dài 2m, người thứ nhất đặt điểm treo của vật cách vai mình 120cm. Bỏ qua trọng lượng của đòn gánh. Hỏi mỗi người chịu một lực là?

Một vật rắn quay quanh một trục cố định xuyên qua vật với phương trình toạ độ góc : \(\varphi=1,5+0,5t\) , trong đó \(\varphi\) tính bằng rađian (rad) và t tính bằng giây (s). Một điểm trên vật và cách trục quay khoảng r =  4 cm thì có tốc độ dài bằng

Chọn đáp án đúng

 Mức vững vàng của cân bằng được xác định bởi

Hai học sinh A và B đứng trên chiếc đu đang quay tròn đều, A ở ngoài rìa, B ở cách tâm một đoạn bằng nửa bán kính của đu. Gọi v_A, v_B, a_A, a_B lần lượt là tốc độ dài và gia tốc dài của A và B. Kết luận nào sau đây là đúng ? 

Có ba chất điểm 5kg, 4kg và 3kg được đặt trong hệ toạ độ 0xy. Vật 5kg có toạ độ (0,0); 3kg có toạ độ (0,4); 4kg có toạ độ (3,0). Hỏi phải đặt vật 8kg ở đâu để khối tâm của hệ trùng với gốc toạ độ (0,0)?

Một đĩa đặc đồng chất, khối lượng 0,2 kg, bán kính 10 cm, có trục quay Δ đi qua tâm đĩa và vuông góc với đĩa, đang đứng yên. Tác dụng vào đĩa một momen lực không đổi 0,02 N.m. Tính quãng đường mà một điểm trên vành đĩa đi được sau 4 s kể từ lúc tác dụng momen lực.

Trong các chuyển động sau, chuyển động của vật nào là chuyển động tịnh tiến?

Gió thổi vào xe theo hướng vuông góc với thành bên của xe với vận tốc V. Xe có khối lượng (m = 10⁴kg ), chiều cao 2b = 2,4m, chiều ngang 2= 2m, chiều dài l = 8m . Áp suất gió tính bởi công thức \(p = \rho v^ 2\) với \(\rho = 1,3kg/m^3\) là khối lượng riêng của không khí. V bằng bao nhiêu để xe bị lật ngã?

 Một vật không có trục quay cố định, khi chịu tác dụng của một ngẫu lực thì vật sẽ như thế nào?

Có 5 quả cầu nhỏ trọng lượng P; 2P; 3P; 4P; 5P gắn lần lượt trên thanh nhẹ, khoảng cách giữa hai quả cầu cạnh nhau là l. Tìm vị trí trọng tâm của hệ.

Một người dùng búa để nhổ một chiếc đinh, khi người đó tác dụng một lực 50N vào đầu búa thì định bắt đầu chuyển động. Biết cánh tay đòn của lực tác dụng của người đó là 20cm và của lực nhổ đinh khỏi gỗ là 2cm. Hãy tính lực cản của gỗ tác dụng vào đinh.