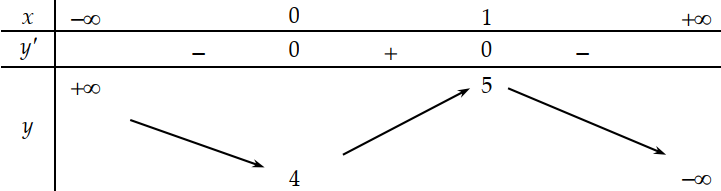Hàm số \(y = 4\sqrt {{x^2} – 2x + 3} + 2x – {x^2}\) đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTa có \(y = 4\sqrt {{x^2} – 2x + 3} + 2x – {x^2} = 4\sqrt {{{\left( {x – 1} \right)}^2} + 2} – {\left( {x – 1} \right)^2} + 1\).
Đặt \(t = {\left( {x – 1} \right)^2} \ge 0\). Xét hàm số \(y = 4\sqrt {t + 2} – t + 1\)
\( \Rightarrow y'(t) = \frac{{2 – \sqrt {t + 2} }}{{\sqrt {t + 2} }} = 0 \Leftrightarrow t = 2.\)
Lập bảng biến thiên của hàm số
.png)
Ta được hàm số đạt giá trị lớn nhất tại \(t = 2 \Leftrightarrow x = 1 \pm \sqrt 2 \). Suy ra \({x_1}{x_2} = – 1\).
ADMICRO
YOMEDIA
ZUNIA9
.jpg.png)