Hình phẳng giới hạn bởi hai đồ thị \(y=|x|\text{ và }y=x^{2}\)quay quanh trục tung tạo nên một vật thể tròn xoay có thể tích bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai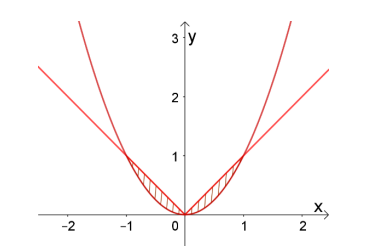
Phương trình hoành độ giao điểm: \(|x|=x^{2} \Leftrightarrow\left[\begin{array}{l} x=0 \Rightarrow y=0 \\ x=\pm 1 \Rightarrow y=1 \end{array}\right.\)
Ta có đồ thị hai hàm số\(y=|x|\text{ và }y=x^{2}\)đều đối xứng qua Oy nên hình phẳng giới hạn bởi hai đồ thị\(y=|x|\text{ và }y=x^{2}\) quay quanh trục tung tạo nên một vật thể tròn xoay có thể tích bằng thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi hai đường \(y=x\,và\,x=\sqrt y\) quay xung quanh trục Oy . Thể tích vật thể tròn xoay cần tìm là:
\(V=\pi \int\limits_{0}^{1}\left|y-y^{2}\right| \mathrm{d} y=\pi \int\limits_{0}^{1}\left(y-y^{2}\right) \mathrm{d} y=\left.\pi \cdot\left(\frac{1}{2} y^{2}-\frac{1}{3} y^{3}\right)\right|_{0}=\frac{\pi}{6}\)











