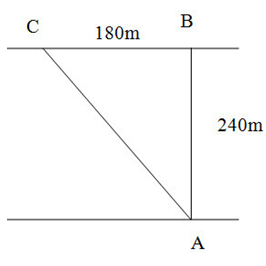
Một máy bay có vận tốc đều trong không khí yên tĩnh là v. Máy bay bay theo chu vi 1 hình vuông cạnh a. Biểu thức của thời gian mà máy bay bay hết 1 vòng của hình vuông trog trường hợp gió thổi vận vốc ko đổi u<v dọc theo đường chéo
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.PNG)
+ Khi gió thổi với vận tốc không đổi u < v dọc theo đường chéo
+ Gỉa sử gió thổi theo hướng đường chéo AC
+ Thời gian để máy bay bay hết một vòng là:
\( t = {t_{AB}} + {t_{BC}} + {t_{CD}} + {t_{DA}}\)
+ Trên hình vẽ ta có:
\(\begin{array}{l} {v_{AB}} = {v_{BC}} = u\cos {45^0} + \sqrt {{v^2} - {{(u\cos {{45}^0})}^2}} \\ \to {v_{AB}} = {v_{BC}} = \frac{{u\sqrt 2 }}{2} + \sqrt {{v^2} - {{(\frac{{u\sqrt 2 }}{2})}^2}} = \frac{{u\sqrt 2 }}{2} + \sqrt {{v^2} - {{\frac{u}{2}}^2}} (1)\\ {v_{CD}} = {v_{DA}} = \sqrt {{v^2} - {{\frac{u}{2}}^2}} - \frac{{u\sqrt 2 }}{2}(2)\\ \to t = 2\frac{a}{{{v_{AB}}}} + 2\frac{a}{{{v_{CD}}}} = \frac{a}{{\frac{{u\sqrt 2 }}{2} + \sqrt {{v^2} - {{\frac{u}{2}}^2}} }} + 2\frac{a}{{\sqrt {{v^2} - {{\frac{u}{2}}^2}} - \frac{{u\sqrt 2 }}{2}}} = \frac{{4a\sqrt {{v^2} - {{\frac{u}{2}}^2}} }}{{{v^2} - {u^2}}} \end{array}\)
+ Khi gió thổi với vận tốc không đổi u<v dọc theo đường chéo thì thời gian để máy bay bay hết một vòng của hình vuông là : \( t = \frac{{4a\sqrt {{v^2} - {{\frac{u}{2}}^2}} }}{{{v^2} - {u^2}}}\)
Câu hỏi liên quan
-
Một tàu hoả chiều dài 110m chuyển động với vận tốc 60km/h. Cần bao nhiêu thời gian để tàu vượt qua hoàn toàn một người đang đi bộ với vận tốc 6km/h ngược chiều trên con đường song song với tàu.
-
Xét sự chuyển động của Trái Đất quanh Mặt Trời và sự tự quay quanh trục của Trái Đất, các vị trí có vận tốc tức thời bằng nhau về độ lớn là các vị trí ứng với những lúc:
-
Hai tàu chở khách chạy ngược chiều nhau trên hai làn đường ray song song sát cạnh nhau. ở một thời điểm hai tàu đi qua hai điểm A và B cách nhau 200km. Biết tốc độ của tàu đi qua A là 60km, tàu đi qua B là 45km/h. Hai tàu sẽ gặp nhau tại thời điểm cách thời điểm chúng đi qua các điểm A và B trên một khoảng
-
Một người nông dân lái canô chuyển động đều và xuôi dòng từ bến A đến bến B mất 2 giờ. Khoảng cách hai bến là 48km, biết vận tốc của nước so với bờ là 8km/h. Tính thời gian để canô quay về từ B đến A.
-
Một chiếu thuyền buồm chạy ngược dòng sông. Sau 1 giờ đi được 20 km , một khúc gỗ trôi theo dòng sông sau 1 phút trôi được 150/3 m. Vận tốc của thuyền buồm so với nước có giá trị là bao nhiêu ?
-
Một chiếc xe ca nô chạy xuôi dòng sông từ A đến B mất 4 giờ. A, B cách nhau 40 km, nước chảy với vận tốc 4 km/h. Tính vận tốc của ca nô đối với nước.
-
Hai bến sông A và B cách nhau 18 km theo đường thẳng. Biết vận tốc của canô khi nước không chảy là 16,2 km/h và vận tốc của nước so với bờ sông là 1,5 m/s . Thời gian canô đi từ A đến B rồi quay trở lại A là:
-
Một canô chạy thẳng đều xuôi dòng từ bến A đến bến B cách nhau 54km mất khoảng thời gian 3h. Vận tốc của dòng chảy là 6km/h. Tính vận tốc của canô đối với dòng chảy.
-
Một người đi xe đạp với vận tốc 14,4 km/h, trên một đoạn đường song hành với đường sắt. Một đoạn tàu dài 120 m chạy ngược chiều và vượt người đó mất 6 s kể từ lúc tàu gặp người đó. Hỏi vận tốc của tàu là bao nhiêu
-
Hai người chèo thuyền với vận tốc không đổi là 4 km/h, lúc đầu chèo ngược dòng chảy của một con sông, biết vận tốc của nước là 1,5 km/h. Hai người đó phải mất bao nhiêu thời gian để đi được 1 km?
-
Hai ô tô A và B đang chạy cùng phương ngược chiều với vận tốc không đổi v. Hỏi người quan sát ở vị trí nào sẽ thấy mình đang chuyển động với vận tốc 2v?
-
Một chiếc thuyền đi trong nước yên lặng với vận tốc có độ lớn v1, vận tốc dòng chảy của nước so với bờ sông có độ lớn v2. Nếu người lái thuyền hướng mũi thuyền dọc theo dòng nước từ hạ nguồn lên thượng nguồn của con sông thì một người đứng trên bờ sẽ thấy
-
Một người bơi từ điểm A của bờ sông bên này sang bờ bên kia của một con sông rộng 100m. Khi người đó bơi theo hướng vuông góc với dòng chảy thì điểm đến bờ bên kia (điểm B) cách vị trí đối diện với A (điểm H) một khoảng 50m. Để người đó sang bờ bên kia tại đúng vị trí đối diện với điểm A thì người đó phải bơi theo hướng tạo với hướng của dòng chảy một góc bằng
-
Tại sao trạng thái đứng yên hay chuyển động của chiếc xe ôtô có tính tương đối?
-
Hai tàu A B ban đầu cách nhau một khoảng là l. CHúng chuyển thẳng đều cùng với một lúc với các vận tốc có độ lớn là v1 v2 . tàu A chuyển động theo hướng AC tạo với AB góc \(\alpha\) như hình vẽ. Muốn hai tàu gặp nhau ở H thì các độ lớn vận tốc v1, v2 phải thỏa mãn điều kiện gì
.PNG)
-
Một người bơi dọc theo chiều dài 50 m của bể bơi hết 40 s, rồi quay lại về chỗ xuất phát trong 42 s. Gọi v1, v2 và v3 lần lượt là tốc độ trung bình: trong lần bơi đầu tiên theo chiều dài của bể bơi; trong lần bể bơi về và trong suốt quãng đường đi và về. Tổng (v1 + v2 + 2v3) gần giá trị nào nhất sau đây?
-
Có 3 điểm nằm dọc theo trục Ox (có chiều từ A đến B) theo thứ tự là A, B và C. Cho AB = 200 m, BC = 300 m. Một người xuất phát từ A qua B đến C. Hỏi quãng đường và độ lớn độ dịch chuyển của người này trong cả chuyến đi là bao nhiêu?
-
Một chiếc thuyền chuyển động thẳng đều với v = 10 m/s so với mặt biển, con mặt biển tĩnh lặng. Một người đi đều trên sàn thuyền có v = 1 m/s so với thuyền. Xác định vận tốc của người đó so với mặt nước biển khi người và thuyền chuyển động cùng chiều.
-
Một người lái ô tô đi thẳng 6 km theo hướng tây, sau đó rẽ trái đi thẳng theo hướng nam 4 km rồi quay sang hướng đông 3 km. Xác định quãng đường đi được và độ lớn độ dịch chuyển tổng hợp của ô tô.
-
Một phi công muốn máy bay của mình bay về hướng Tây, trong khi gió thổi về hướng Nam với vận tốc v=50km/h . Biết rằng khi không có gió, vận tốc của máy bay là 200km/h . Vận tốc của máy bay so với mặt đất là:
