Một sợi dây đang có sóng dừng ổn định. Sóng truyền trên dây có tần số 10 Hz và bước sóng 6 cm. Trên dây, hai phần tử M và N có vị trí cân bằng cách nhau 8 cm, M thuộc một bụng sóng dao động điều hòa với biên độ 6 mm. Lấy \({{\pi }^{2}}=10.\) Tại thời điểm t, phần tử M đang chuyển động với tốc độ \(6\pi \text{ cm/s}\) thì phần tử N chuyển động với gia tốc có độ lớn là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTần số góc: \(\omega =2\pi f=20\pi \text{ rad/s}\text{.}\)
Gọi A là biên độ dao động của bụng sóng.
Điểm N cách bụng M một khoảng 8 cm \(\Rightarrow MN=\frac{4}{3}\lambda =\frac{\lambda }{4}+\lambda +\frac{\lambda }{12}\Rightarrow\)N cách điểm nút gần nhất khoảng \(\frac{\lambda }{12}\Rightarrow\) điểm N dao động với biên độ \({{A}_{N}}=\frac{A}{2}=3\text{ mm}.\)
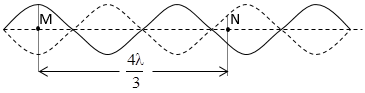
Dựa vào hình vẽ, ta có M và N dao động ngược pha nhau nên \[\left| \frac{{{a}_{N}}}{{{a}_{M}}} \right|=\frac{{{A}_{N}}}{{{A}_{M}}}=\frac{1}{2}\Rightarrow \left| {{a}_{N}} \right|=\frac{\left| {{a}_{M}} \right|}{2}\text{ m/}{{\text{s}}^{2}}.\]
Áp dụng hệ thức độc lập cho điểm M taị thời điểm t: \(\frac{v_{M}^{2}}{{{\omega }^{2}}}+\frac{a_{M}^{2}}{{{\omega }^{4}}}=A_{M}^{2}\Rightarrow \left| {{a}_{M}} \right|=12\sqrt{3}\text{ m/}{{\text{s}}^{2}}.\)
Độ lớn gia tốc của điểm N tại thời điểm t: \[\left| {{a}_{N}} \right|=\frac{\left| {{a}_{M}} \right|}{2}=\frac{12\sqrt{3}}{2}=6\sqrt{3}\text{ m/}{{\text{s}}^{2}}.\]











