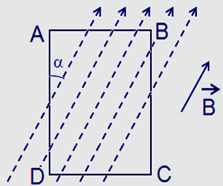
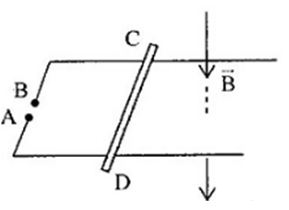
Một thanh kim loại CD có chiều dài l=20cm khối lượng m=100g đặt vuông góc với 2 thanh ray song song nằm ngang và nối với nguồn điện như hình vẽ. Hệ thống đặt trong từ trường đều có B=0,2T phương chiều như vẽ, dòng điện I= 10A có chiều từ D đến C. Biết hệ số ma sát giữa CD và thanh ray là μ=0,1. Bỏ qua điện trở của các thanh ray, điện trở tại nơi tiếp xúc và dòng điện cảm ứng trong mạch. Nâng hai đầu thanh AB của ray lên để hợp với mặt phẳng ngang góc 300. Xác định gia tốc chuyển động của thanh bắt đầu trượt với vận tốc ban đầu bằng 0.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
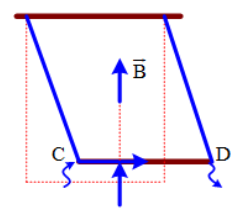
Báo saiTa có, các lực tác dụng lên thanh gồm: trọng lực \(\vec P\) , lực ma sát \(\overrightarrow {{F_{ms}}} \), phản lực \(\vec N\) và lực từ \(\vec F\) có hướng như hình vẽ:
.png) + Áp dụng định luật II – Niuton, ta có:
+ Áp dụng định luật II – Niuton, ta có:
\(\vec N + \vec P + \overrightarrow {{F_{ms}}} + \vec F = m\vec a\)
Chiếu (*) lên các phương ta được:
\(\left\{ \begin{array}{l}
Ox:Psin\alpha - Fcos\alpha - Fms = ma(1)\\
Oy:N - Pcos\alpha - Fsin\alpha = 0(2)
\end{array} \right.\)
Từ (2) ta suy ra: \(N = Pcos\alpha + Fsin\alpha \)
+ Lực ma sát: \({F_{ms}} = \mu N = \mu \left( {Pcos\alpha + F\sin \alpha } \right)\)
Lực từ:\({F_{ms}} = \mu \left( {Pcos\alpha + BIl\sin \alpha } \right)\)
⇒ Lực ma sát: \({F_{ms}} = \mu \left( {Pcos\alpha + BIl\sin \alpha } \right)\)
Thay vào (1) ta được:
\(\begin{array}{*{20}{l}} {P\sin \alpha - BIlcos\alpha - \mu \left( {Pcos\alpha + BIl\sin \alpha } \right) = ma}\\ { \Rightarrow a = \frac{{P\left( {\sin \alpha - \mu cos\alpha } \right) - BIl\left( {cos\alpha + \mu \sin \alpha } \right)}}{m}}\\ { = \frac{{0,1.10\left( {\sin {{30}^0} - 0,1.cos{{30}^0}} \right) - 0,2.10.0,2\left( {cos{{30}^0} + 0,1.\sin {{30}^0}} \right)}}{{0,1}}}\\ { \approx 0,47m/{s^2}} \end{array}\)
.png)