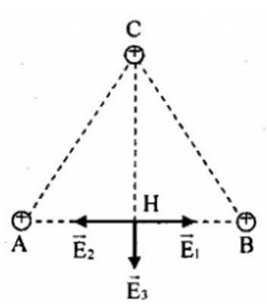
Tại ba đỉnh của tam giác đều ABC, cạnh a=10cm có ba điện tích điểm bằng nhau và bằng 10nC. Hãy xác định cường độ điện trường tại trung điểm của cạnh AB.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai+ Gọi H - trung điểm của cạnh AB
+ Gọi \( \overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) lần lượt là cường độ điện trường do diện tích \(q_1,q_2,q_3\) gây tại H
+ Ta có:, các vecto \( \overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) được biểu diễn như hình
Ta có: \( {E_1} = {E_2} = k\frac{{\left| q \right|}}{{{{\left( {\frac{{AB}}{2}} \right)}^2}}};{E_3} = k\frac{{\left| q \right|}}{{C{H^2}}}\)
Lại có: \( CH = \sqrt {C{B^2} - B{H^2}} = \sqrt {C{B^2} - {{\left( {\frac{{AB}}{2}} \right)}^2}} = \sqrt {{{10}^2} - {{\left( {\frac{{10}}{2}} \right)}^2}} = 5\sqrt 3 cm\)
Ta suy ra: \( {E_3} = {9.10^9}\frac{{{{10.10}^{ - 9}}}}{{{{(5\sqrt 3 {{.10}^{ - 2}})}^2}}} = 12000V/m\)
+ Ta có cường độ điện trường tổng hợp tại H: \( \overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \)
+ Vì: \(\left\{ \begin{array}{l} \overrightarrow E \uparrow \downarrow \overrightarrow {{E_1}} \\ {E_1} = {E_2} \end{array} \right. \to \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = \overrightarrow 0 \)
+ Ta suy ra: \( \overrightarrow {{E}} = \overrightarrow {{E_3}} \to E=E_3=12000V/m\)
Câu hỏi liên quan
-
Véctơ cường độ điện trường tại mỗi điểm có chiều:
-
Trong các quy tắc vẽ các đường sức điện sau đây, quy tắc nào sai ?
-
Tại hai điểm A và B cách nhau 20 cm trong không khí có đặt hai điện tích \(q_1=4.10^{−6}; q_2=−6.10^{−6}\) . Xác định cường độ điện trường do hai điện tích điểm này gây ra tại C, biết AC = 12 cm, BC = 16 cm. Xác định lực điện tác dụng lên điện tích \(q_3=−5.10^{−8}\)đặt tại C.
-
Tính chất cơ bản của điện trường là tác dụng
-
Với trường tĩnh điện, khẳng định nào sau đây sai?
-
Chọn câu đúng
-
Một prôtôn và một electron lần lượt được tăng tốc từ trạng thái đứng yên trong một điện trường đều. Biết prôtôn và electron có độ lớn điện tích bằng nhau, khối lượng prôtôn lớn hơn khối lượng electron. Khi prôtôn và electron đi được những quãng đường bằng nhau thì
-
Tại điểm nào sẽ không có điện trường?
-
Phát biểu nào sau đây là không đúng?
-
Chọn phát biểu sai:
-
Cho hai điện tích điểm q1 = q2 C đặt tại hai điểm cố định A, B cách nhau một khoảng 2a m trong không khí. Trên đường trung trực của AB tại vị trí mà cường độ điện trường có cường độ cực đại. Giá trị cực đại đó là
-
Đường sức điện cho biết
-
Đơn vị của cường độ điện trường
-
Cho hình vuông ABCD cạnh a, tại A và C đặt các điện tích \(q_1=q_3=q<0\). Cần đặt ở B điện tích bằng bao nhiêu để cường độ điện trường ở D bằng 0.
-
Chiếu một bức xạ có bước sóng 0,48 µm lên một tấm kim loại có công thoát là 2,4.10-19J. Dùng màn chắn tách ra một chùm hẹp các electron quang điện và cho chúng đi vào không gian có điện trường đều, theo hướng vectơ cường độ điện trường. Biết cường độ điện trường có giá trị 1000V/m. Quãng đường tối đa mà electron chuyển động được theo chiều vectơ cường độ điện trường là:
-
Trong các nhận xét sau, nhận xét nào không đúng với đặc điểm của đường sức điện?
-
Cường độ điện trường của một điện tích phụ thuộc vào khoảng cách r được mô tả như đồ thị bên. Biết \( {r_2} = \frac{{{r_1} + {r_3}}}{2}\) và các điểm cùng nằm trên một đường sức. Giá trị của x bằng
-
Nếu tại một điểm có 2 điện trường gây bởi 2 điện tích điểm Q1 âm và Q2 dương thì hướng của cường độ điện trường tại điểm đó được xác định bằng
-
Phát biểu nào sau đây không đúng?
-
Chọn phát biểu sai?
