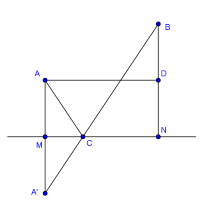
Thành phố Hải Đông dự định xây dựng một trạm nước sạch để cung cấp cho hai khu dân cư (A ) và (B ). Trạm nước sạch đặt tại vị trí (C ) trên bờ sông. Biết \( AB = 3\sqrt {17} km\), khoảng cách từ (A ) và (B ) đến bờ sông lần lượt là (AM = 3km ), (BN = 6km)(hình vẽ). Gọi (T ) là tổng độ dài đường ống từ trạm nước đến (A ) và (B ). Tìm giá trị nhỏ nhất của (T )

Câu hỏi liên quan

• Mệnh đề nào sau đây là sai?

• Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình \((x-2)^{2}+(y-2)^{2}=4\) Phép đồng dạng có được bằng cách thực hiện liên tiếp các phép vị tự có tâm O tỉ số \(k=\frac{1}{2}\) và phép quay tâm O góc 90⁰ sẽ biến (C) thành đường tròn nào trong các đường tròn sau?

• Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn  (C₁): x²+y²−2x−2y−2 = 0 và (C₂): x²+y²+12x−16y = 0. Phép đồng dạng F tỉ số k  biến (C₁) thành(C₂). Tìm k?

ZUNIA12

• Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình x+y-2=0. Viết phương trình đường thẳng d ' là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I (-1;-1) tỉ số \(k=\frac{1}{2}\) và phép quay tâm O góc \(-45^{0}\).

• Trong mặt phẳng Oxy cho đường thẳng d: 2x - y =0 thỏa mãn phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = -2 và phép đối xứng trục Oy sẽ biến đường thẳng d thành đường thẳng nào sau đây?

• Cho tam giác ABC và A'B'C' đồng dạng với nhau theo tỉ số k . Mệnh đề nào sau đây là sai?

• Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 3 và phép đối xứng trục Ox, biến đường thẳng d: x - y - 1 = 0 thành đường thẳng d’ có phương trình.

• Trong mặt phẳng tọa độ Oxy cho hai điểm \(A(-2 ;-3) \text { và } B(4 ; 1)\) Phép đồng dạng tỉ số \(k=\frac{1}{2}\) biến điểm A thành A′, biến điểm B thành B′. Tính độ dài A'B′

• Mọi phép dời hình cũng là phép đồng dạng với tỉ số k bằng:

• Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:

  

   

• Phóng to một hình chữ nhật kích thước là 4 và 5 theo phép đồng dạng tỉ số k = 3 thì được hình có diện tích là bao nhiêu?

• Giả sử phép đồng dạng F biến tam giác ABC thành tam giác A'B'C'. Giả sử F biến trung tuyến AM của tam giác ABC thành đường cao A'M' của tam giác A'B'C'. Mệnh đề nào sau đây là đúng?

• Cho hình chữ nhật ABCD có tâm I. Gọi H, K, L, J lần lượt là trung điểm của AD, BC, KC, IC. Tứ giác IHCD đồng dạng với tứ giác nào sau đây?

• Cho hình chữ nhật ABCD và AC = 2AB. Gọi Q là phép quay tâm A góc quay \(\varphi = (AB,AC)\). V là phép vị tự tâm  tỉ số 2, F là phép hợp thành của V và Q. F biến đường tròn tâm B bán kính BA thành đường tròn nào sau đây?

• Mệnh đề nào sau đây là sai?

• Cho điểm I(2;1) điểm M(-1;0) phép đồng dạng hợp thành bởi phép vị tự tâm I tỉ số k = -2 và phép đối xứng trục Ox biến M thành M’’ có tọa độ.

• Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0)  tỉ số k = \(\frac{1}{2}\) và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ: 

• Mệnh đề nào sau đây là sai?

• Trong mặt phẳng tọa độ Oxy cho điểm M (2;4). Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số \(k=\frac{1}{2}\) và phép đối xứng qua trục Oy sẽ biến M thành điểm nào trong các điểm sau:

• Cho tam giác ABC có đường cao AH, H nằm giữa B và C. Biết AH = 4, HB = 2, HC = 8. Phép đồng dạng F biến tam giác HBA thành tam giác HAC. F được hình thành bởi hai phép biến hình nào?