Tìm tất cả các giá trị thực của tham số m để phương trình \(m+{{e}^{\frac{x}{2}}}=\sqrt[4]{{{e}^{2x}}+1}\) có nghiệm thực:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiBiến đổi phương trình về dạng \(m=\sqrt[4]{{{\left( {{e}^{x}} \right)}^{2}}+1}-\sqrt{{{e}^{x}}}\). Đặt \(t={{e}^{x}};(t>0)\) ta xét hàm số \(y=\sqrt[4]{{{t}^{2}}+1}-\sqrt{t}\) trên \(\left( 0;+\infty\right)\).
\(y'=\frac{t}{2.\sqrt[4]{{{\left( {{t}^{2}}+1 \right)}^{3}}}}-\frac{1}{2\sqrt{t}}\)\(=\frac{\sqrt{{{t}^{3}}}-\sqrt[4]{{{\left( {{t}^{2}}+1 \right)}^{3}}}}{2.\sqrt{t}.\sqrt[4]{{{\left( {{t}^{2}}+1 \right)}^{3}}}}=\frac{\sqrt[4]{{{\left( {{t}^{2}} \right)}^{3}}}-\sqrt[4]{{{\left( {{t}^{2}}+1 \right)}^{3}}}}{2.\sqrt{t}.\sqrt[4]{{{\left( {{t}^{2}}+1 \right)}^{3}}}}<0\)(\(\forall t>0)\)
BBT
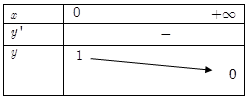
Vậy điều kiện cần tìm là 0 < m < 1











