Tìm tất cả các giá trị thực của tham số m để phương trình \(m+e^{\frac{x}{2}}=\sqrt[4]{e^{2 x}+1}\) có nghiệm thực:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(PT\Leftrightarrow m=\sqrt[4]{\left(e^{x}\right)^{2}+1}-\sqrt{e^{x}}\)
Đặt \(t=e^{x} ;(t>0)\)
Ta xét hàm số \(y=\sqrt[4]{t^{2}+1}-\sqrt{t} \text { trên }(0 ;+\infty)\)
Ta có:\(y^{\prime}=\frac{t}{2 \cdot \sqrt[4]{\left(t^{2}+1\right)^{3}}}-\frac{1}{2 \sqrt{t}}=\frac{\sqrt{t^{3}}-\sqrt[4]{\left(t^{2}+1\right)^{3}}}{2 \cdot \sqrt{t} \cdot \sqrt[4]{\left(t^{2}+1\right)^{3}}}=\frac{\sqrt[4]{\left(t^{2}\right)^{3}}-\sqrt[4]{\left(t^{2}+1\right)^{3}}}{2 \cdot \sqrt{t} \cdot \sqrt[4]{\left(t^{2}+1\right)^{3}}}<0(\forall t>0)\)
Bảng biến thiên
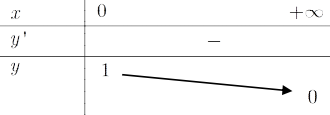
Vậy điều kiện cần tìm là 0<m<1
ADMICRO
YOMEDIA
ZUNIA9











