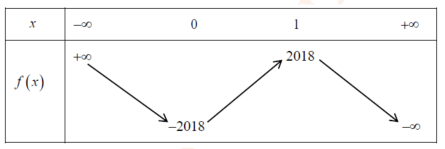
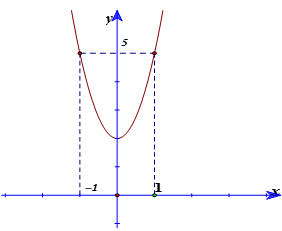
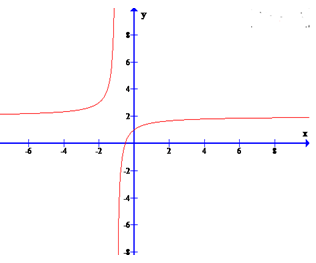
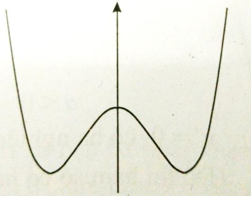
Cho hàm số f có đạo hàm trên khoảng I. Xét các mệnh đề sau:
(I). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyyzImRaaGimaaaa!3BF1! f'\left( x \right) \ge 0\), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiaIiIaam % iEaiabgIGiolaadMeaaaa!3A13! \forall x \in I\) (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I) thì hàm số đồng biến trên I.
(II). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0\),\(\forall x \in I\) (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I) thì hàm số nghịch biến trên I.
(III). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0; \forall x \in I\) thì hàm số nghịch biến trên khoảng I.
(IV). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0, \forall x \in I\) và f'(x) = 0 tại vô số điểm trên I thì hàm số f không thể nghịch biến trên khoảng I.
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?

.png)
.png)