Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình x+y-2=0. Viết phương trình đường thẳng d ' là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I (-1;-1) tỉ số \(k=\frac{1}{2}\) và phép quay tâm O góc \(-45^{0}\).
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi 1 d là ảnh của d qua phép vị tự tâm I(-1;-1) tỉ số \(k=\frac{1}{2}\)
Vì \(d_{1}\) song song hoặc trùng với d nên phương trình của nó có dạng \(x+y+c=0\).
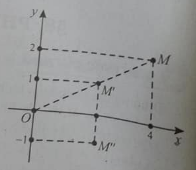
Lấy M (1;1) thuộc d.
Gọi \(M^{\prime}\left(x^{\prime} ; y^{\prime}\right)=V_{\left(I ; \frac{1}{2}\right)}(M) \longleftrightarrow \overrightarrow {I M^{\prime}}=\frac{1}{2} \overrightarrow{I M} \Rightarrow\left\{\begin{array}{l} x+1=\frac{1}{2}(1+1) \\ y+1=\frac{1}{2}(1+1) \end{array}\right.\)
\(\Rightarrow M^{\prime}(0 ; 0) \in d_{1}\) .
Vậy phương trình của \(d_{1}\) là x+y = 0.
Ảnh của \(d_{1}\) (đường phân giác góc phần tư thứ hai) qua phép quay tâm O góc \(-45^{0}\) là đường thẳng Oy. Vậy phương trình của d ' là x = 0.