Trong mặt phẳng tọa độ Oxy , cho đường tròn . Ảnh của đường tròn qua việc thực hiện liên tiếp phép tịnh tiến theo véc tơ và phép quay tâm O , góc quay là
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiGọi I là tâm đường tròn và (C') là ảnh của (C) khi thực hiện liên tiếp phép tịnh tiến theo véc tơ và phép quay tâm O, góc quay .
Gọi là ảnh của I khi thực hiện phép tịnh tiến theo véc tơ .
Ta có .
Gọi là ảnh của khi thực hiện phép quay tâm O, góc quay
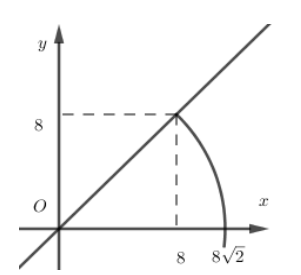
Suy ra . Do đó là ảnh của I khi thực hiện liên tiếp phép tịnh tiến theo véc tơ và phép quay tâm O, góc quay hay là tâm của (C').
Hơn nữa, phép quay và phép tịnh tiến đều bảo toàn khoảng cách nên .
Vậy có (C') phương trình là .
ADMICRO
YOMEDIA
ZUNIA9











