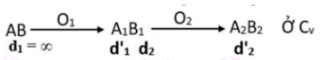Vật kính của kính hiển vi có tiêu cự f1=0,8cm , thị kính có tiêu cự f2=2cm Khoảng cách giữa hai kính là a=16cm . Một người mắt không tật quan sát một vật nhỏ qua kính trong trạng thái ngắm chừng ở vô cực. Tính khoảng cách nhỏ nhất giữa hai điểm A, B trên vật mà mắt người còn phân biệt được khi nhìn qua kính. Biết năng suất phân ly của mắt ε=1/3500(rad)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai+ Quá trình tạo ảnh của kính hiển vi giống như quá trình tạo ảnh qua hệ hai thấu kính ghép đồng trục và được tóm tắt qua sơ đồ sau:
+ Khi ngắm chừng ảnh A2B2A2B2 ở điểm cực viễn của mắt, ta có:
\(d_2′=∞⇒d_2=f_2=2cm\)
\( d{'_1} = \overline {{O_1}{A_1}} = a - {d_2} = 16 - 2 = 14cm\)
\( \to {d_1} = \overline {{O_1}A} = \frac{{d{'_1}.{f_1}}}{{d{'_1} - {f_1}}} = \frac{{14.0,8}}{{14 - 0.8}} = \frac{{28}}{{33}}\)
+ Mắt trông ảnh A2B2 dưới góc trông α . Để phân biệt được hai điểm A, B qua kính tức phân biệt ảnh 2 A2B2 của nó, muốn vậy \(α≥ε\)
+ Ta có \( \alpha \approx \tan \alpha = \frac{{{A_2}{B_2}}}{{\left| {d{'_2}} \right|}} \ge \varepsilon \to {A_2}{B_2} \ge \left| {d{'_2}} \right|\varepsilon \)
+ Mặt khác: \( \frac{{{A_2}{B_2}}}{{AB}} = \frac{{{A_2}{B_2}}}{{{A_1}{B_1}}}.\frac{{{A_1}{B_1}}}{{AB}} = \left| {\frac{{{d_2}'}}{{{d_2}}}} \right|\left| {\frac{{{d_1}'}}{{{d_1}}}} \right| \to {A_2}{B_2} = \left| {\frac{{{d_2}'}}{{{d_2}}}} \right|\left| {\frac{{{d_1}'}}{{{d_1}}}} \right|AB(2)\)
+ Từ (1) và (2) suy ra:
\( \left| {\frac{{{d_2}'}}{{{d_2}}}} \right|\left| {\frac{{{d_1}'}}{{{d_1}}}} \right|AB \ge \left| {d{'_2}} \right|\varepsilon \to AB \ge \left| {\frac{{{d_2}{d_1}}}{{{d_1}'}}} \right|\varepsilon = \frac{1}{{3500}}.\frac{{2.\frac{{28}}{{33}}}}{{24}} = {3,46.10^{ - 5}}cm\)